19. Прогнозирование на основе моделей трендов
Для выявления тренда необходимо предварительно оценить вероятность его существования. Существует множество разных методов выявления существования тенденции, но в данном пособии рассмотрим два – метод разности средних уровней и метод Фостера-Стюарта.
Метод разности средних уровней
Метод разности средних уровней – самый естественный подход при выявлении существования тренда.
Динамический ряд делится на две части, примерные равные по количеству элементов ряда, и каждая часть рассматривается как самостоятельная выборка. Испытание разности средних показывает, существенно ли различие между средними или расхождение можно приписать случайным факторам, определить как случайность и сделать вывод об отсутствии тренда.
Для малого числа наблюдений используется модификация метода, основанная на критерии Стьюдента. Если tрасч меньше tтабл (рассчитанного для степени вероятности a и числа степеней свободы n1+n2-2), то с уверенностью можно говорить об отсутствии тренда.
Критерий Стьюдента применяется в том случае, если между дисперсиями частей временного ряда наблюдается несущественное различие. Расчетное значение критерий Стьюдента будет определяться по формуле:
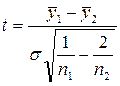 , (2.1)
, (2.1)
Где 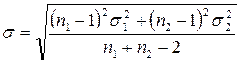 ;
;
![]() - среднее квадратическое отклонение соответственно по первой и второй выборке данных.
- среднее квадратическое отклонение соответственно по первой и второй выборке данных.
Близость дисперсий проверяют с помощью критерия Фишера при условии, что большая дисперсия стоит в числителе отношения. Дисперсии по выборкам будут считаться однородными, если выполняется условие: Fрасч<Fтабл.
Метод разности средних уровней применяется в большинстве случаев для выявления тенденции, но ему присущи следующие недостатки:
1) данный метод применим только для рядов с монотонной тенденцией;
2) этот метод нечувствителен к небольшому тренду.
Поэтому далее рассмотрим второй метод – метод Фостера Стюарта.
| < Предыдущая | Следующая > |
|---|