14. Решение типовых задач с помощью ППП «Excel»
1. Настройка пакета для выполнения регрессионного анализа
Процедуры корреляционно-регрессионного анализа выполняются в табличном процессоре с помощью модуля «Пакет анализа». Для подключения этого модуля с помощью команды СЕРВИС – НАДСТРОЙКИ выведите окно НАДСТРОЙКИ и включите надстройку ПАКЕТ АНАЛИЗА.
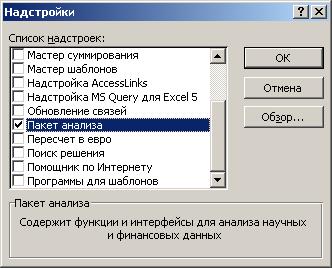
Рис. 11. Диалоговое окно Надстройки меню Сервис.
После выполнения этой процедуры в ниспадающем меню пункта СЕРВИС появится команда АНАЛИЗ ДАННЫХ.
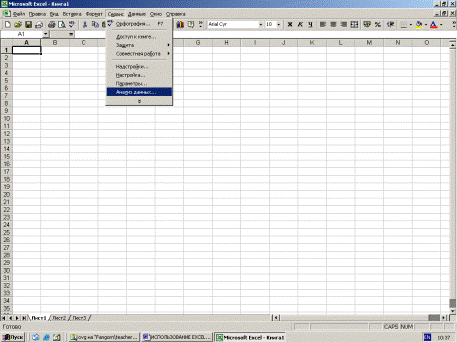
Рис. 12. Лист ППП «Excel» пункт меню Сервис команда Анализ данных.
2. Расчет показателей описательной статистики
Для проверки требований, предъявляемых к исходным данным, следует рассчитать ряд показателей, характеризующих эти данные (среднее значение, дисперсия и т. д.). Эти характеристики данных можно получить, воспользовавшись функцией СЕРВИС - АНАЛИЗ ДАННЫХ – ОПИСАТЕЛЬНАЯ СТАТИСТИКА.
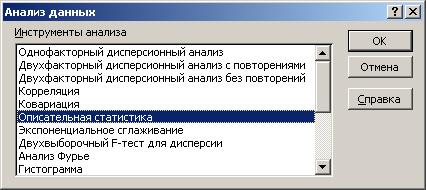
Рис. 13. Диалоговое окно АНАЛИЗ ДАННЫХ.
После выбора требуемой функции откроется окно ОПИСАТЕЛЬНАЯ СТАТИСТИКА.
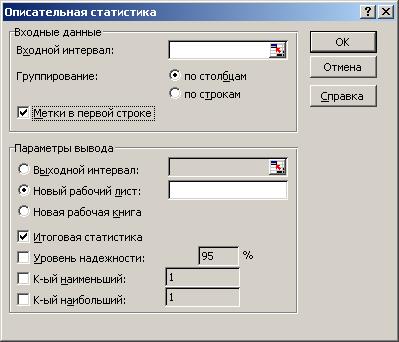
Рис. 14. Диалоговое окно ОПИСАТЕЛЬНАЯ статистика.
Для расчета показателей описательной статистики в окне «Входной интервал» укажите область ячеек электронной таблицы, где расположены анализируемые данные (исследуемый показатель и все факторы). Желательно в эту область включить ячейки с обозначениями переменных (Х0, Х1, …, Хр) для комфортного восприятия результатов вычислений. Если метки данных (обозначения переменных) учтены, то в области ВХОДНЫЕ ДАННЫЕ включите опцию «Метки в первой строке». Затем в области «Параметры вывода» укажите, куда должны быть выведены результаты расчетов (Новый лист либо Выходной интервал И верхняя левая ячейка области электронной таблицы, где должны быть размещены результаты).
В области «Параметры вывода» включите опцию «Итоговая статистика» и выполните процедуру.
В полученных результатах расчетов удалите повторяющуюся информацию (многократное повторение названий статистик) и рассчитайте для каждого показателя коэффициенты вариации (по среднему значению и стандартному отклонению).
3. Выявление тесноты связи и закона зависимости между факторами и результирующим показателем (анализ полей корреляции)
Для построения полей корреляции (диаграмм рассеивания) используйте команду ВСТАВКА – ДИАГРАММА – ТОЧЕЧНАЯ (вариант без соединения точек) либо мастер диаграмм. В результате выполнения этой команды появится окно МАСТЕР ДИАГРАММ (шаг 2 из 4):
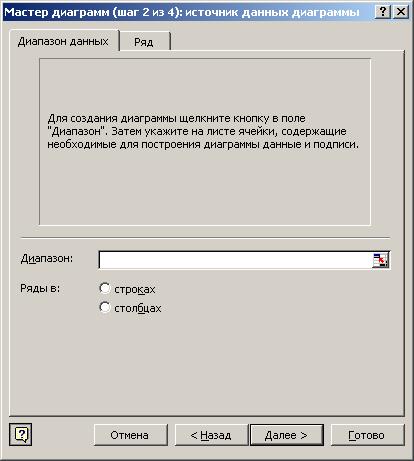
Рис. 15. Диалоговое окно Мастера диаграмм.
В окне Диапазон укажите область столбца электронной таблицы, где находится массив данных для фактора, и через точку с запятой область данных по результирующему показателю. Щелкните мышкой по кнопке ДАЛЕЕ. В результате появится окно следующего 3 шага. В соответствующих окнах введите заголовок графика и названия осей; разместите график на рабочем листе. Постройте графики, отражающие влияние каждого фактора на исследуемый показатель.
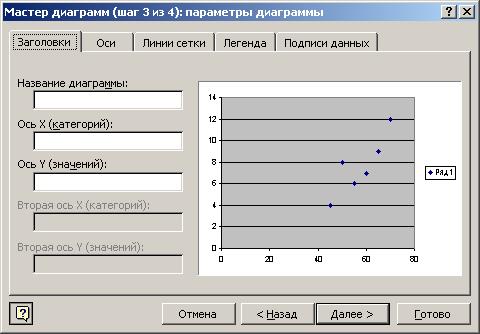
Рис. 16. Диалоговое окно Мастера диаграмм – Параметры диаграммы.
Элементы корреляционной матрицы получите, воспользовавшись функцией СЕРВИС - АНАЛИЗ ДАННЫХ - КОРРЕЛЯЦИЯ. В результате будет открыто окно АНАЛИЗ ДАННЫХ.
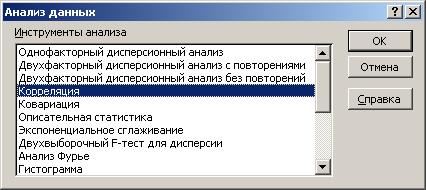
Рис. 17. Диалоговое окно Анализ данных.
После выбора требуемой функции откроется окно КОРРЕЛЯЦИЯ.
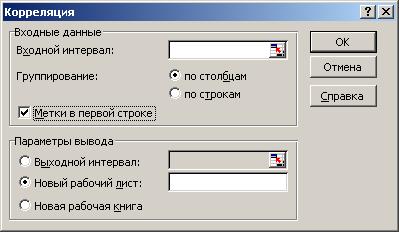
Рис. 18. Диалоговое окно Корреляция.
В окне «Входной интервал» задайте область ячеек электронной таблицы, где расположены анализируемые данные (исследуемый показатель и все факторы). В эту область так же включите ячейки с обозначениями переменных (Х0, Х1, …, Хр). Если метки учтены в области данных, то в окне КОРРЕЛЯЦИЯ включите опцию «Метки в первой строке». Затем в области «Параметры вывода» укажите левую верхнюю ячейку области электронной таблицы, куда должна быть выведена корреляционная матрица.
Анализируя корреляционную матрицу, сделайте выводы о том, как сильно связаны факторы между собой и с исследуемым показателем. Если обнаружены коллинеарные (мультиколлинеарные) факторы, то для дальнейшего анализа следует оставить только один из этих факторов. Проводя анализ взаимосвязей показателей по корреляционной матрице, необходимо помнить о том, что парные коэффициенты корреляции - это показатели тесноты связи для линейных зависимостей.
4. Расчет параметров регрессионной модели
Вид регрессионной модели обосновывают двумя путями: теоретическим и эмпирическим. В первом случае используют качественные рассуждения о законе связи между исследуемым показателем и каждым из факторов, а также результаты других исследователей по построению аналогичных регрессионных моделей. При эмпирическом подходе выводы о форме связи делают на основе анализа фактических данных, представленных в виде первичных полей корреляции.
Чаще всего для анализа используют линейный вид модели или модель, которую можно привести к линейному виду путем некоторых преобразований и замены переменных.
Для расчета параметров регрессионной модели воспользуйтесь функцией СЕРВИС - АНАЛИЗ ДАННЫХ - РЕГРЕССИЯ. В результате появится окно АНАЛИЗ ДАННЫХ. В этом окне выберите инструмент анализа РЕГЕРССИЯ.
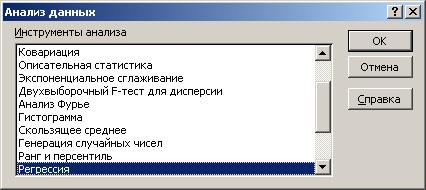
Рис. 19. Диалоговое окно Анализ данных.
После щелчка мышкой по кнопке ОК на экране появится окно РЕГРЕССИЯ.
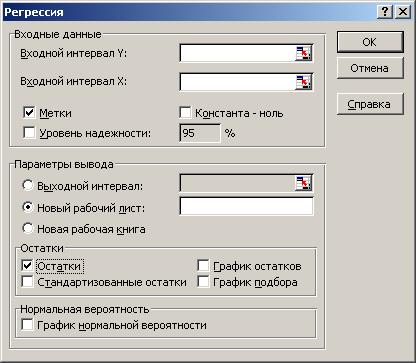
Рис. 20. Диалоговое окно Регрессия.
В этом окне в области «Входной интервал Y» укажите область ячеек, где находятся данные исследуемого показателя, в области «Входной интервал X» - область ячеек с данными по всем факторам. Желательно при этом учитывать обозначения переменных. Если метки данных включены при определении области переменных, то включите опцию «Метки».
Чтобы получить данные для расчета средней относительной ошибки аппроксимации, в этом диалоговом окне поставьте флажок рядом с опцией ОСТАТКИ.
В результате использования функции СЕРВИС - АНАЛИЗ ДАННЫХ - РЕГРЕССИЯ будут получены не только параметры модели, но и показатели, позволяющие оценить надежность построенной модели.
5. Исключение из модели факторов, оказывающих несущественной влияние
Все факторы, влияние которых на исследуемый показатель несущественно, должны быть исключены из модели. Влияние фактора следует считать несущественным, если соответствующий коэффициент регрессии статистически не значим, то есть его можно приравнять нулю. Коэффициент регрессии ![]() следует считать статистически значимым (не равным нулю), если фактическая величина критерия Стьюдента будет больше табличного значения этого критерия. Табличное значение критерия Стьюдента можно найти, воспользовавшись в Excel мастером функций
следует считать статистически значимым (не равным нулю), если фактическая величина критерия Стьюдента будет больше табличного значения этого критерия. Табличное значение критерия Стьюдента можно найти, воспользовавшись в Excel мастером функций ![]() .
.
После обращения к мастеру функций на экране появится окно «Мастер функций – шаг 1 из 2».
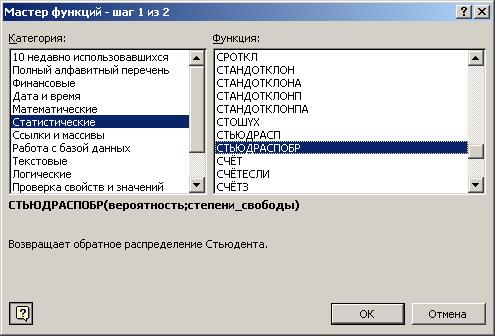
Рис. 21. Диалоговое окно Мастера функций.
В левой части этого окна выберите категорию функций «Статистические», в правой части, используя бегунок, выберите функцию «СТЬЮДРАСПРОБР» и щелкните мышкой по кнопке ОК. В результате появится окно для задания параметров этой функции. В этом окне «Вероятность» – уровень значимости ![]() (
(![]() = 1-
= 1-![]()
![]() , где
, где ![]() - доверительная вероятность).
- доверительная вероятность).
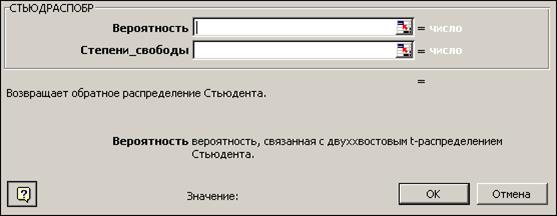
Рис. 22. Диалоговое окно функции Стьюдраспобр.
Уровень значимости ![]() обычно принимают равным 0,05; число степеней свободы
обычно принимают равным 0,05; число степеней свободы ![]() =
= ![]() (где
(где ![]() - число наблюдений,
- число наблюдений, ![]() - число параметров регрессионной модели).
- число параметров регрессионной модели).
Если в модели присутствует несколько несущественных факторов, то первым следует исключить тот фактор, для которого табличное значение критерия Стьюдента ![]() намного больше
намного больше ![]() . Несущественно влияющий фактор убирают из совокупности наблюдений и пересчитывают параметры регресcионной модели и ее характеристики. Для модели, полученной на втором шаге, заново проверяют статистическую значимость коэффициентов регресcии. Если вновь обнаружен фактор, оказывающий несущественное влияние на анализируемый показатель, то этот фактор также исключают из модели. Отсев факторов из модели выполняют до тех пор, пока в ней останутся только факторы, оказывающие сильное влияние на
. Несущественно влияющий фактор убирают из совокупности наблюдений и пересчитывают параметры регресcионной модели и ее характеристики. Для модели, полученной на втором шаге, заново проверяют статистическую значимость коэффициентов регресcии. Если вновь обнаружен фактор, оказывающий несущественное влияние на анализируемый показатель, то этот фактор также исключают из модели. Отсев факторов из модели выполняют до тех пор, пока в ней останутся только факторы, оказывающие сильное влияние на ![]() .
.
Чтобы убедиться в том, что из модели были исключены факторы, оказывающие слабое влияние на исследуемый показатель, сравните величины коэффициентов детерминации первого и последнего шагов. Их различие будет незначительным.
6. Проверка надежности регрессионной модели
Вывод о статистической значимости модели в целом делают по ![]() - критерию. Если фактическая величина критерия Фишера окажется больше табличного значения, то полученная модель статистически значима и полно описывает изменение исследуемого показателя под действием факторов, присутствующих в модели.
- критерию. Если фактическая величина критерия Фишера окажется больше табличного значения, то полученная модель статистически значима и полно описывает изменение исследуемого показателя под действием факторов, присутствующих в модели.
Теоретическое значение ![]() - критерия также можно получить с помощью мастера функций
- критерия также можно получить с помощью мастера функций ![]() . Для этого в окне «Мастер функций – шаг 1 из 2» следует выбрать функцию FРАСПОБР.
. Для этого в окне «Мастер функций – шаг 1 из 2» следует выбрать функцию FРАСПОБР.

Рис. 23. Диалоговое окно Мастера функций.
В окне выбранной функции задайте требуемые параметры.

Рис. 24. Диалоговое окно функции Fраспобр.
«Вероятность» – уровень значимости ![]()
![]() (обычно принимают равным 0,05); «Число_степеней свободы1» - это число факторов, присутствующих в модели, «Число_степеней свободы2» определяют как разность между числом наблюдений и числом параметров модели.
(обычно принимают равным 0,05); «Число_степеней свободы1» - это число факторов, присутствующих в модели, «Число_степеней свободы2» определяют как разность между числом наблюдений и числом параметров модели.
Если Fрасч > Fтабл, то построенная модель считается статистически надежной, а следовательно, правильно отражает закон изменения исследуемого показателя под действием факторов, присутствующих в модели.
7. Проверка адекватности регрессионной модели
Среднюю относительную ошибку аппроксимации пользователь должен рассчитать самостоятельно по формуле  , где
, где ![]() фактические (расчетные) значения исследуемого показателя.
фактические (расчетные) значения исследуемого показателя.
Если модель используют для целей анализа, допустима величина средней относительной ошибки до 10%, при применении модели для прогнозирования ошибка не должна быть больше 4%.
Для этого рядом с остатками следует добавить столбец фактических значений исследуемого показателя и выполнить ряд промежуточных расчетов.
8. Интерпретация полученных результатов
На этом этапе разрабатывают рекомендации об использовании результатов регрессионного анализа. Анализируют коэффициенты регрессии в натуральном и стандартизованном масштабе, а также коэффициенты эластичности.
Коэффициент регрессии в натуральном масштабе ![]() показывает, на сколько своих единиц измерения в среднем изменится исследуемый показатель
показывает, на сколько своих единиц измерения в среднем изменится исследуемый показатель ![]() при увеличении
при увеличении ![]() - го фактора на единицу своего измерения. При этом влияние остальных факторов находится на среднем уровне; свободный член уравнения характеризует изменение показателя за счет изменения факторов, неучтенных в модели.
- го фактора на единицу своего измерения. При этом влияние остальных факторов находится на среднем уровне; свободный член уравнения характеризует изменение показателя за счет изменения факторов, неучтенных в модели.
В связи с тем, что факторы имеют различный физический смысл и различные единицы измерения, коэффициенты регрессии ![]() нельзя сравнивать между собой и, следовательно, невозможно определить, какой из факторов оказывает наибольшее влияние. Для устранения различий в единицах измерения применяют частные коэффициенты эластичности, рассчитываемые по формуле:
нельзя сравнивать между собой и, следовательно, невозможно определить, какой из факторов оказывает наибольшее влияние. Для устранения различий в единицах измерения применяют частные коэффициенты эластичности, рассчитываемые по формуле: 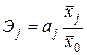 , где
, где ![]() - средние значения
- средние значения ![]() - го фактора и исследуемого показателя,
- го фактора и исследуемого показателя, ![]() - коэффициент регрессии, стоящий при переменной
- коэффициент регрессии, стоящий при переменной ![]() в многофакторном уравнении регрессии. Как известно, коэффициент эластичности характеризующие на сколько % в среднем изменится
в многофакторном уравнении регрессии. Как известно, коэффициент эластичности характеризующие на сколько % в среднем изменится ![]() При увеличении j-го фактора на 1% при фиксированном положении других факторов.
При увеличении j-го фактора на 1% при фиксированном положении других факторов.
При определении степени влияния отдельных факторов необходим показатель, который бы учитывал влияние анализируемых факторов с учетом различий в уровне их колеблемости. Таким показателем является коэффициент регрессии в стандартизированном масштабе 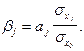 Коэффициент
Коэффициент ![]() показывает на какую часть своего среднеквадратического отклонения изменится
показывает на какую часть своего среднеквадратического отклонения изменится ![]() при изменении j-го фактора на одно свое среднеквадратическое отклонение при фиксированном значении остальных факторов. Уравнение регрессии в стандартизированном масштабе :
при изменении j-го фактора на одно свое среднеквадратическое отклонение при фиксированном значении остальных факторов. Уравнение регрессии в стандартизированном масштабе : ![]() где
где 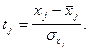
Границы влияния фактора на исследуемый показатель рассчитываются по формуле ![]() (левая граница)
(левая граница) ![]() (правая граница), где
(правая граница), где ![]() - доверительные полуинтервалы.
- доверительные полуинтервалы.
| < Предыдущая | Следующая > |
|---|