13. Решение типовых задач
Задача 1.3.
По 30 территориям России имеются данные, представленные в табл. 1.12.
Таблица 1.12
|
Признак |
Среднее значение |
Среднее квадратическое отклонение |
Линейный коэффициент парной корреляции |
|
Среднедневной душевой доход, руб., у |
86,8 |
11,44 |
- |
|
Среднедневная заработная плата 1 работающего, руб., х1 |
54,9 |
5,86 |
|
|
Средний возраст безработного, лет, х2 |
33,5 |
0,58 |
Требуется:
1. Построить уравнение множественной регрессии в стандартизованном и в натуральном виде; рассчитать частные коэффициенты эластичности, сравнить их с b1 и b2, пояснить различия между ними.
2. Рассчитать линейные коэффициенты частной корреляции и коэффициент множественной корреляции, сравнить их с линейными коэффициентами парной корреляции, пояснить различия между ними.
3. Рассчитать общий и частные F-критерии Фишера.
1. Линейное уравнение множественной регрессии Y от X1 и X2 имеет вид: 
. Для расчета его параметров применим метод стандартизации переменных и построим искомое уравнение в стандартизованном масштабе: 
.
Расчет b-коэффициентов выполним по формулам:
;
.
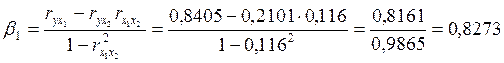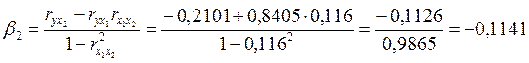Получим уравнение: 
.
Для построения уравнения в естественной форме рассчитаем B1 и B2, используя формулы для перехода от BI к Bi:
; 
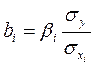; (1.37)
; 
.
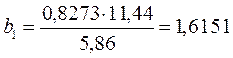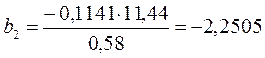Значение А определим из соотношения:
,
.
Для характеристики относительной силы влияния Х1 и Х2 на У рассчитаем средние коэффициенты эластичности:
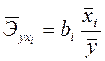; (1.38)
; 
.
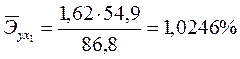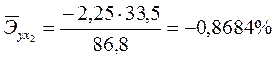С увеличением средней заработной платы Х1 на 1 % от ее среднего уровня средний душевой доход У возрастает на 1,02% от своего среднего уровня; при повышении среднего возраста безработного Х2 на 1% среднедушевой доход У снижается на 0,87% от своего среднего уровня. Очевидно, что сила влияния средней заработной платы Х1 на средний душевой доход У оказалась большей, чем сила влияния среднего возраста безработного Х2. К аналогичным выводам о силе связи приходим при сравнении модулей значений B1 и B2:
.
Различия в силе влияния фактора на результат, полученные при сравнении 
и 
, объясняются тем, что коэффициент эластичности исходит из соотношения средних, а b-коэффициент – из соотношения средних квадратических отклонений.
2. Линейные коэффициенты частной корреляции в этой задаче будут рассчитываться по рекуррентной формуле 1.31:
;
;
.
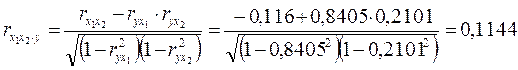Если сравнить значения коэффициентов парной и частной корреляции, то приходим к выводу, что из-за слабой межфакторной связи (
) коэффициенты парной и частной корреляции отличаются незначительно: выводы о тесноте и направлении связи на основе коэффициентов парной и частной корреляции совпадают:
; 
; 
;
; 
; 
.
Расчет линейного коэффициента множественной корреляции выполним с использованием коэффициентов 
и 
:
, (1.39)
.
Зависимость У от Х1 и Х2 характеризуется как тесная, в которой 72% вариации среднего душевого дохода определяются вариацией учтенных в модели факторов: средней заработной платы и среднего возраста безработного. Прочие факторы, не включенные в модель, составляют соответственно 28% от общей вариации У.
3. Общий F-критерий проверяет гипотезу Н0 о статистической значимости уравнения регрессии и показателя тесноты связи (R2=0):
, (1.40)
; 
; 
.
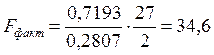Сравнивая Fтабл и Fфакт, приходим к выводу о необходимости отклонить гипотезу Н0, так как Fтабл=3,4<Fрасч=34,6. С вероятностью 1-A=0,95 Делаем заключение о статистической значимости уравнения в целом и показателя тесноты связи 
, которые сформировались под неслучайным воздействием факторов Х1 и Х2.
Частные F-критерии - 
и 
оценивают статистическую значимость присутствия факторов Х1 и Х2 в уравнении множественной регрессии, оценивают целесообразность включения в уравнение одного фактора после другого фактора, т. е. 
оценивает целесообразность включения в уравнение фактора Х1 после того, как в него был включен фактор Х2. Соответственно 
указывает на целесообразность включения в модель фактора Х2 после фактора Х1:
;
; .
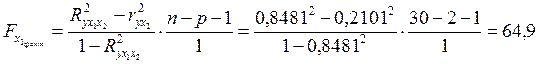Сравнивая FТабл и FФакт, приходим к выводу о целесообразности включения в модель фактора Х1 после фактора Х2, так как 
. Гипотезу Н0 о несущественности прироста 
за счет включения дополнительного фактора Х1 отклоняем и приходим к выводу о статистически подтвержденной целесообразности включения фактора Х1 после фактора Х2.
Целесообразность включения в модель фактора Х2 после фактора Х1 проверяем :
.
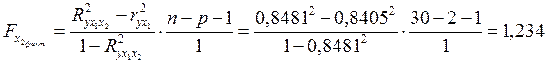Низкое значение 
(немногим больше 1) свидетельствует о статистической незначимости прироста 
за счет включения в модель фактора Х2 после фактора Х1. Следовательно, подтверждается нулевая гипотеза Н0 о нецелесообразности включения в модель фактора Х2 (средний возраст безработного). Это означает, что парная регрессионная модель зависимости среднего дохода от средней заработной платы является достаточно статистически значимой, надежной и что нет необходимости улучшать ее, включая дополнительный фактор Х2 (средний возраст безработного).
Задача 1.4.
По 20 территориям России изучаются следующие данные (табл. 1.13): зависимость среднегодового душевого дохода У (тыс. руб.) от доли занятых тяжелым физическим трудом в общей численности занятых Х1 (%) и от доли экономически активного населения в численности всего населения Х2 (%).
Таблица 1.13
|
Признак |
Среднее значение |
Среднее квадратическое отклонение |
Характеристика тесноты связи |
Уравнение связи |
|
У |
112,76 |
31,58 |
|
|
|
Х1 |
5,40 |
3,34 |
|
|
|
Х2 |
50,88 |
1,74 |
|
|
Требуется:
1. Составить таблицу дисперсионного анализа для проверки при уровне значимости A=0,05 статистической значимости уравнения множественной регрессии и его показателя тесноты связи.
2. С помощью частных F-критериев Фишера оценить, насколько целесообразно включение в уравнение множественной регрессии фактора Х1 после фактора Х2 и насколько целесообразно включение Х2 после Х1.
3. Оценить с помощью T-критерия Стьюдента статистическую значимость коэффициентов при переменных Х1 и Х2 множественного уравнения регрессии.
1. Задача дисперсионного анализа состоит в проверке нулевой гипотезы Н0 о статистической незначимости уравнения регрессии в целом и показателя тесноты связи.
Анализ выполняется при сравнении фактического и табличного (критического) значения F-критерия Фишера Fтабл и Fфакт. Fфакт определяется из соотношения значений факторной и остаточной дисперсий, рассчитанных на одну степень свободы:
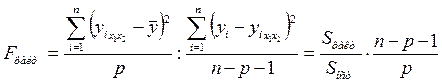, (1.41)
Где N – число единиц совокупности;
P – число факторов в уравнении линейной регрессии;
- фактические значения результативного признака;
- расчетные значения результативного признака.
Результаты дисперсионного анализа представлены в табл. 1.14.
Таблица 1.14
|
Вариация результата, У |
Число степеней свободы |
Сумма квадратов отклонений, S |
Дисперсия на одну степень свободы, S2 |
Fфакт |
Fтабл, A=0,05, k1=2, k2=17 |
|
Общая |
Df=n-1=19 |
19945,9 | |||
|
Факторная |
K1=p=2 |
11918,3 |
5959,15 |
12,62 |
3,59 |
|
Остаточная |
K2=n-p-1=17 |
8027,6 |
472,21 |
;
;
;
.
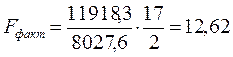Сравнивая Fтабл и Fфакт приходим к выводу о необходимости отклонить гипотезу Н0 и сделать вывод о статистической значимости уравнения регрессии в целом и значения 
, так как они статистически надежны.
2. Частный F-критерий Фишера оценивает статистическую целесообразность включения фактора Х1 в модель после того, как в нее включен фактор Х2. Частный F-критерий Фишера строится как отношение прироста факторной дисперсии за счет дополнительно включенного фактора (на одну степень свободы) к остаточной дисперсии (на одну степень свободы), подсчитанной по модели с включенными факторами Х1 и Х2:
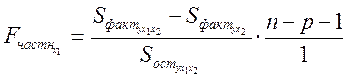. (1.42)
Результаты дисперсионного анализа представлены в табл. 1.15.
Таблица 1.15
|
Вариация результата, У |
Число степеней свободы |
Сумма квадратов отклонений, S |
Дисперсия на одну степень свободы, S2 |
Fфакт |
Fтабл, A=0,05, k1=2, k2=17 |
|
Общая |
Df=n-1=19 |
19945,9 | |||
|
Факторная, в т. ч. - за счет Х2; - за счет дополнительно включенного Х1. |
K1=p=2 1 1
|
11918,3 5127,1 6791,2 |
5959,15 5127,1 6791,2 |
12,62 10,86 14,38 |
3,59 4,45 4,45 |
|
Остаточная |
K2=n-p-1=17 |
8027,6 |
472,21 |
;
;
;
;
.
Включение фактора Х1 после фактора Х2 оказалось статистически значимым и оправданным: прирост факторной дисперсии (в расчете на одну степень свободы) оказался существенным, т. е. следствием дополнительного включения в модель систематически действующего фактора Х1, так как 
.
Аналогично проверим целесообразность включения в модель дополнительного фактора Х2 после включенного ранее фактора Х1. Расчет выполним с использованием показателей тесноты связи и 
:
.
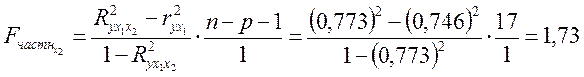В силу того, что 
, приходит к выводу, что включение х2 после х1 оказалось бесполезным: прирост факторной дисперсии в расчете на одну степень свободы был несуществен, статистически незначим, т. е. влияние х2 не является устойчивым и систематическим.
3. Оценка с помощью T-критерия Стьюдента значимости коэффициентов B1 и B2 Связана с сопоставлением их значений с величиной их случайных ошибок: 
и 
. Расчет значений случайных ошибок достаточно сложен, поэтому предлагается более простой способ: расчет значения T-критерия Стьюдента для коэффициентов регрессии линейного уравнения как квадратного корня из соответствующего частного F-критерия Фишера:
;
.
Табличные (критические) значения T-критерия Стьюдента зависят от принятого уровня значимости A (обычно это 0,1; 0,05 или 0,01) и от числа степеней свободы (n-p-1), где N – число единиц совокупности, P – число факторов в уравнении.
В нашем примере при A=0,05; df=20-3=17; tтабл=2,10. Сравнивая Tтабл и Tфакт, приходим к выводу, что так как 
, коэффициент регрессии B1 является статистически значимым, надежным. Так как 
, то величина B2 является статистически незначимой, из-за того, что она формируется в основном под воздействием случайных факторов.
Задача 1.5.
Дана корреляционная матрица, n=20, табл. 1.16.
Таблица 1.16
|
|
Y |
X1 |
X2 |
X3 |
X4 |
X5 |
X6 |
X7 |
X8 |
X9 |
|
Y |
1 | |||||||||
|
X1 |
0,736 |
1 | ||||||||
|
X2 |
-0,222 |
-0,025 |
1 | |||||||
|
X3 |
-0,125 |
0,168 |
0,065 |
1 | ||||||
|
X4 |
-0,146 |
-0,493 |
-0,190 |
-0,104 |
1 | |||||
|
X5 |
0,559 |
0,938 |
0,102 |
0,155 |
-0,679 |
1 | ||||
|
X6 |
0,384 |
-0,291 |
-0,386 |
-0,462 |
0,355 |
-0,423 |
1 | |||
|
X7 |
-0,315 |
-0,268 |
0,093 |
-0,310 |
-0,428 |
0,024 |
0,017 |
1 | ||
|
X8 |
0,215 |
0,611 |
0,005 |
0,043 |
-0,214 |
0,582 |
-0,367 |
-0,297 |
1 | |
|
X9 |
-0,322 |
-0,308 |
0,184 |
-0,215 |
-0,456 |
-0,007 |
0,079 |
0,921 |
-0,337 |
1 |
Требуется:
Провести анализ коллинеарности и мультиколлинеарности факторов. И отобрать факторы для построения регрессионной модели.
Решение
Два фактора находятся в сильной линейной зависимости друг от друга, то есть считаются коллинеарными, если парный коэффициент корреляции между ними больше 0,8. Корреляционная матрица состоит из парных коэффициентов корреляции. Итак, из всей факторов коллинеарными будут Х1 и Х5 
, а также Х7 и Х9 
. Возникает вопрос - какие же из этих факторов необходимо исключить из модели? Для этого сравним по каждой паре коллинеарных факторов парные коэффициенты корреляции, которые показывают тесноту связи между исследуемыми факторами и результирующим показателем У.
; 
Значение парного коэффициента корреляции между результирующим показателем У и фактором Х1 больше значения парного коэффициента корреляции между У и Х5, следовательно, теснота связи между У и Х5 меньше, чем между У и Х1. Поэтому фактор Х5 можно исключить из дальнейшего анализа. По этой же схеме проанализируем и вторую пару коллинеарных факторов - Х7 и Х9.
; 
Необходимо помнить, что отрицательный знак при коэффициенте парной корреляции показывает только направление связи, поэтому в этом случае такие парные коэффициенты корреляции сравниваются между собой в абсолютном значении, то есть по модулю:
.
Как видно из неравенства Х7 слабее связан с результирующим показателем, чем Х9, поэтому фактор Х7 исключается из дальнейшего анализа.
Теперь, когда в нашем наборе факторов не осталось коллинеарных, необходимо определить какие факторы останутся для построения регрессионной модели. Для этого проверяем коэффициенты парной корреляции каждого из оставшихся факторов с результирующим показателем на надежность с помощью T-критерия Стьюдента. Число степеней свободы для парного коэффициента корреляции равно n-2.
; 
; 
.
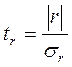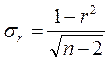Результаты анализа надежности парных коэффициентов корреляции представлены в табл. 1.17.
Таблица 1.17
|
Фактор |
Парный коэффициент корреляции между фактором и результирующим показателем у |
Стандартная ошибка, sr |
Tрасч |
Tтабл |
|
X1 |
0,736 |
0,108 |
6,81 |
2,10 |
|
X2 |
-0,222 |
0,224 |
0,99 |
2,10 |
|
X3 |
-0,125 |
0,232 |
0,54 |
2,10 |
|
X4 |
-0,146 |
0,231 |
0,63 |
2,10 |
|
X6 |
0,384 |
0,201 |
1,91 |
2,10 |
|
X8 |
0,215 |
0,225 |
0,96 |
2,10 |
|
X9 |
-0,322 |
0,211 |
1,52 |
2,10 |
Фактор будет считаться надежным, если Tрасч>tтабл. Этому условию удовлетворяет только один показатель – Х1. Остальные все исключаются из модели, так как не имеют практически никакого влияния на результирующий показатель. Поэтому для построения регрессионной модели выбираем один фактор Х1, и уравнением регрессии будет уравнение прямой: 
.
| < Предыдущая | Следующая > |
|---|
