3.5. Коррекция статистических выводов при автокоррелированности ошибок
· 3.5. Коррекция статистических выводов при автокоррелированности ошибок
Пусть мы имеем дело с наблюдениями, производимыми последовательно через равные промежутки времени (ежедневные, еженедельные, ежеквартальные, ежегодные статистические данные) и выявляем по графику зависимости стандартизованных остатков 
от 
тенденцию Сохранения знака Соседних наблюдений. В таком случае мы можем подозревать Нарушение условия независимости случайных ошибок 
в принятой нами модели наблюдений
В форме положительной автокоррелированности ряда ошибок.
Простейшей моделью автокоррелированности ошибок является Модель авторегрессии первого порядка:
Где 
, а 
— независимые в совокупности случайные величины, имеющие одинаковое нормальное распределение 
. Тогда гипотеза
Соответствует (при нашем предположении о нормальности распределения случайных ошибок) Независимости в совокупности случайных величин 
. В качестве альтернативной используем гипотезу
Соответствующую Положительной автокоррелированности случайных величин (т. е. Тенденции преимущественного сохранения знака случайной ошибки при переходе от - го наблюдения к 
-му). Если гипотеза Отклоняется критерием Дарбина-Уотсона в пользу альтернативной гипотезы То для получения правильных статистических выводов относительно коэффициентов модели необходима соответствующая коррекция.
Итерационная процедура Кохрейна-Оркатта (Cochrane-Orcutt).
Умножим обе части выражения для 
-го наблюдения на 
, так что
И вычтем обе части полученного выражения из соответствующих частей выражения для -го наблюдения:
Тем самым мы приходим к преобразованной модели наблюдений
Где
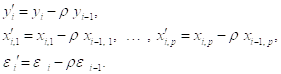
Поскольку в принятой модели ошибок
То это означает, что ошибки 
в преобразованной модели — независимые в совокупности случайные величины, имеющие одинаковое нормальное распределение .
Иными словами, Случайные ошибки в преобразованной модели удовлетворяют стандартным предположениям. Следовательно, В рамках преобразованной модели никакой дополнительной коррекции обычных статистических выводов о коэффициентах модели не требуется. Проблема только в том, что используемое в процессе преобразования модели значение коэффициента нам Не известно. Поэтому реально провести указанное преобразование невозможно. Вместо этого можно пытаться заменить указаное преобразование какой-либо его аппроксимацией с заменой неизвестного значения на его оценку по данным наблюдений. Конечно, при использовании такой аппроксимации мы уже не можем гарантировать, что в преобразованной модели будут независимыми в совокупности случайными величинами, однако есть некоторая надежда на то, что эти ошибки все же будут обнаруживать Меньшую автокоррелированность по сравнению с ошибками в исходной модели.
Описываемая здесь процедура Кохрейна-Оркатта использует для получения аппроксимации теоретического преобразования оценку для в виде
Где 
— остатки, получаемые при оценивании Исходной модели наблюдений. Аппроксимирующее преобразование определяется соотношениями
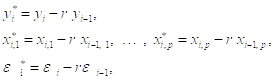
Которые приводят к преобразованной модели
Если в последней модели автокоррелированность не проявляется, то полученные в рамках этой модели оценки параметров 
можно принять в качестве Уточненных оценок параметров 
. Если же в преобразованной модели еще остается выраженная автокоррелированность, то процесс преобразования применяют уже к Преобразованной модели и еще раз уточняют значения параметров и т. д., пока последовательно уточняемые значения параметров не перестанут изменяться в пределах заданной точности.
Заметим, наконец, что обычно мы предполагаем, что
. Соответственно, для первой объясняющей переменной получаем
Так что фактически мы имеем преобразованную модель
С 
. Получив в этой модели оценку 
для 
, мы можем оценить параметр 
исходной модели, просто полагая
Пример. Проанализируем статистические данные о совокупных потребительских расходах (CONS) и денежной массе (MONEY) в США за 1952—1956 г. г. (квартальные данные, в млрд. долларов).
|
Obs |
MONEY |
CONS |
Obs |
MONEY |
CONS |
|
1952:1 |
159.3 |
214.6 |
1954:3 |
173.9 |
238.7 |
|
1952:2 |
161.2 |
217.7 |
1954:4 |
176.1 |
243.2 |
|
1952:3 |
162.8 |
219.6 |
1955:1 |
178.0 |
249.4 |
|
1952:4 |
164.6 |
227.2 |
1955:2 |
179.1 |
254.3 |
|
1953:1 |
165.9 |
230.9 |
1955:3 |
180.2 |
260.9 |
|
1953:2 |
167.9 |
233.3 |
1955:4 |
181.2 |
263.3 |
|
1953:3 |
168.3 |
234.1 |
1956:1 |
181.6 |
265.6 |
|
1953:4 |
169.7 |
232.3 |
1956:2 |
182.5 |
268.2 |
|
1954:1 |
170.5 |
233.7 |
1956:3 |
183.3 |
270.4 |
|
1954:2 |
171.6 |
236.5 |
1956:4 |
184.3 |
275.6 |
Результаты оценивания линейной модели наблюдений
В которой 
— значения объясняемой переменной CONS, а 
- значения объясняющей переменной MONEY, приведены в следующей таблице:
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
Prob. |
|
1 |
–154.719 |
19.850 |
-7.794 |
0.0000 |
|
X |
2.300 |
0.114 |
20.080 |
0.0000 |
|
R-squared |
0.957 |
Durbin-Watson stat |
0.328 |
Хотя коэффициент детерминации весьма близок к единице, значение статистики Дарбина-Уотсона достаточно мало, и это дает возможность подозревать наличие положительной автокоррелированности ошибок в принятой модели наблюдений. Два следующих графика дают представление о рассеянии значений переменных и о поведении остатков.
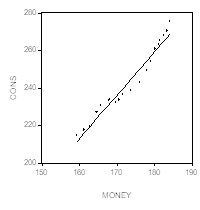
Здесь наблюдаются серии остатков, имеющих одинаковые знаки, что как раз и характерно для моделей, в которых имеется положительная автокоррелированность ошибок.
Для подтверждения положительной автокоррелированности ошибок используем критерий Дарбина-Уотсона. По таблицам находим нижнюю границу для критического значения 
при 
: 
. Полученное при оценивании модели значение 
существенно меньше этой нижней границы, так что гипотеза 
Отвергается в пользу альтернативной гипотезы 
. Для коррекции статистических выводов используем процедуру Кохрейна-Оркатта.
Прежде всего находим оценку для неизвестного значения коэффициента : 
Основываясь на этой оценке, переходим к преобразованной модели, оценивание которой дает следующие результаты:
|
Included observations: 19 after adjusting endpoints | ||||
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
Prob. |
|
1 |
-30.777 |
14.043 |
-2.192 |
0.0426 |
|
X’ |
2.795 |
0.609 |
4.593 |
0.0003 |
|
R-squared |
0.554 |
Durbin-Watson stat |
1.667 |
Хотя в преобразованной модели коэффициент детерминации существенно ниже, чем в непреобразованной модели, значение статистики Дарбина-Уотсона теперь Превышает верхнюю границу 
для критического значения , соответствующего 
. (В преобразованной модели наблюдений на единицу меньше, чем в исходной, так как при преобразовании используются Запаздывающие Значения обеих переменных). Поэтому гипотеза о независимости в совокупности ошибок в преобразованной модели не отвергается (в пользу гипотезы об их положительной автокоррелированности). Два следующих графика дают представление о рассеянии значений преобразованных переменных и о поведении остатков в преобразованной модели.
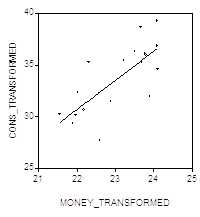
RESID: TRANSFORMED MODEL
Обратим внимание на существенно более нерегулярное поведение остатков по сравнению с исходной моделью.
Обращаясь к результатам оценивания коэффициентов в преобразованной модели, отметим значительное (более, чем в 5 раз!) возрастание оценки стандартной ошибки 
, что подтверждает сделанное ранее замечание о Занижении стандартных ошибок при неучете имеющейся в действительности положительной автокорреляции случайных ошибок в модели наблюдений. Столь существенное возрастание значения приводит к возрастанию более, чем в 5 раз, и ширины доверительного интервала Для мультипликатора 
. Если при оценивании исходной линейной модели 95%-доверительный интервал для этого параметра имел вид 
, то при оценивании преобразованной модели мы получаем интервал 
.
Рассмотренный пример ясно демонстрирует опасность пренебрежения возможной неадекватностью построенной модели в отношении стандартных предположений об ошибках и необходимость Обязательного проведения в процессе подбора подходящей модели связи между теми или иными экономическими факторами Анализа остатков, полученных при оценивании выбранной модели.
Более того, используя преобразованную модель, можно получить Улучшенную модель для прогнозирования объемов расходов на потребление при планируемых объемах денежной массы. Поясним это на примере простой линейной модели
Предполагая, что 
и используя оценку 
для коэффициента , переходим к преобразованной модели
C 
и 
И получаем в рамках этой модели оценки и 
параметров и , так что оцененная модель линейной связи между преобразованными переменными имеет вид
В исходных переменных последние соотношения принимают вид
Где 
, откуда получаем:
Если мы собираемся теперь прогнозировать будущее значение
, соответствующее плановому значению 
объясняющей переменной, то естественно воспользоваться полученным соотношением и предложить в качестве прогнозного дляЗначение
При таком способе вычисления прогнозного значения для Учитывается тенденция сохранения знака остатков: если в последнем наблюдении наблюдавшееся значение 
Превышало значение 
предсказываемое линейной моделью связи 
то и последующее значение Прогнозируется с превышением значения 
предсказываемого этой линейной моделью связи при 
. Если же значение Меньше, чем то тогда будущее значение прогнозируется Меньшим значения 
Пример. Продолжим рассмотрение предыдущего примера. В этом примере 
, 
. Наблюдавшимся значениям 
можно сопоставить:
· Наблюдавшиеся значения 
;
· значения
Получаемые по модели, построенной Без учета автокоррелированности ошибок;
· значения
Получаемые по модели, параметры которой скорректированы С учетом автокоррелированности ошибок;
· значения
Отличающиеся от значений, указанных в предыдущем пункте, Учетом Значения остатка в предшествующем наблюдении.
Ниже приведены графики значений 
, получаемых указанными тремя методами, и графики соответствующих им расхождений 
. Индексы 1, 2, 3 указывают на один из трех способов получения значений , в том порядке, в котором они были перечислены выше).
Сравним средние квадраты расхождений 
При использовании указанных трех методов вычисления значений . Эти средние квадраты равны, соответственно,
Что говорит о большей гибкости прогноза, построенного по последнему (третьему) методу.
Рассмотрим еще одно важное следствие автокоррелированности ошибок в линейной модели
С 
Преобразование
Приводит к модели наблюдений
На основании которой получаем соотношение
Вспомним теперь о нашем предположении, что 
, и преобразуем последнее соотношение следующим образом:
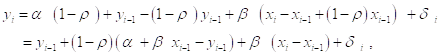Или
Здесь 
, 
и 
. Второе слагаемое в правой части по-существу поддерживает «долговременную» линейную связь (тенденцию)
Если в момент 
отклонение 
от 
положительно 
, то второе слагаемое будет Отрицательным, действуя в сторону Уменьшения приращения . Если же отклонение 
от 
Отрицательно 
, то второе слагаемое будет Положительным, действуя в сторону Увеличения приращения 
.
Указанная модель коррекции приращений переменной 
использует «истинные» значения параметров 
. Поскольку эти значения нам не известны, мы в состоянии построить только Аппроксимацию такой модели, использующую оценки параметров. При этом естественно воспользоваться оценкой 
и уточненными оценками 
, полученными на базе преобразованной модели.
В рассмотренном примере аппроксимирующая модель коррекции приращений принимает вид
| < Предыдущая | Следующая > |
|---|
