3.6. Коррекция статистических выводов при наличии сезонности. Фиктивные переменные
· 3.6. Коррекция статистических выводов при наличии сезонности. Фиктивные переменные
Приведенный ниже график показывает динамику изменения совокупного располагаемого дохода DPI И объемов продаж SALES лыжного инвентаря в США (квартальные данные; DPI — В Млрд Долларов, SALES — в Млн Долларов, в ценах 1972 г.).

Оценивание линейной модели связи указанных переменных дает следующие результаты.
|
Dependent Variable: SALES | ||||
|
Method: Least Squares | ||||
|
Sample: 1964:1 1973:4 | ||||
|
Included observations: 40 | ||||
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
Prob. |
|
C |
29.97613 |
6.463626 |
4.637665 |
0.0000 |
|
DPI |
0.108402 |
0.036799 |
2.945768 |
0.0055 |
|
R-squared |
0.185904 |
Mean dependent var |
48.94571 | |
|
Adjusted R-squared |
0.164481 |
S. D. dependent var |
3.852032 | |
|
S. E. of regression |
3.521017 |
Akaike info criterion |
5.404084 | |
|
Sum squared resid |
471.1074 |
Schwarz criterion |
5.488528 | |
|
Log likelihood |
–106.0817 |
F-statistic |
8.677546 | |
|
Durbin-Watson stat |
1.874403 |
Prob (F-statistic) |
0.005475 |
Коэффициент при переменной ![]() статистически значим. Однако график стандартизованных остатков (приведенный для удобства в двух формах)
статистически значим. Однако график стандартизованных остатков (приведенный для удобства в двух формах)

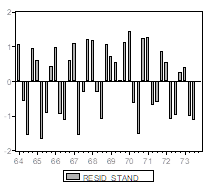
Обнаруживает явную неадекватность построенной модели имеющимся наблюдениям. Однако характер этой неадекватности таков, что он не улавливается критерием Дарбина-Уотсона: значение ![]() статистики Дарбина-Уотсона близко к
статистики Дарбина-Уотсона близко к ![]() . И это не удивительно: за положительными остатками с равным успехом следуют как положительные, так и отрицательные остатки, что соответствует практическому отсутствию корреляции между соседними ошибками и подтверждается диаграммой рассеяния
. И это не удивительно: за положительными остатками с равным успехом следуют как положительные, так и отрицательные остатки, что соответствует практическому отсутствию корреляции между соседними ошибками и подтверждается диаграммой рассеяния

(Здесь ![]() — переменная, образованная остатками от подобранной модели линейной связи, а
— переменная, образованная остатками от подобранной модели линейной связи, а ![]() — переменная, образованная запаздывающими на один квартал значениями переменной
— переменная, образованная запаздывающими на один квартал значениями переменной ![]() .)
.)
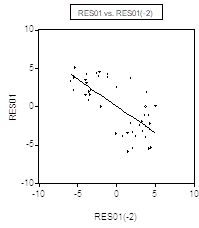

В то же время, налицо отрицательная коррелированность остатков для наблюдений, отстоящих на два квартала, и положительная — для наблюдений, отстоящих на четыре квартала:
В отличие от критерия Дарбина-Уотсона, критерий Бройша-Годфри «замечает» такую коррелированность: допуская коррелированность ошибок для наблюдений, разделенных двумя кварталами, получаем ![]() , что ведет к безусловному отклонению гипотезы о независимости ошибок.
, что ведет к безусловному отклонению гипотезы о независимости ошибок.
Обратим теперь внимание на весьма специфическое поведение остатков. Все остатки, соответствуюшие первому и четвертому кварталам, Положительны, а все (за исключением двух) остатки, соответствующие второму и третьему кварталам, Отрицательны. Такое положение, конечно, просто отражает тот факт, что спрос на зимний спортивный инвентарь возрастает в осенне-зимний период и снижается в весенне-летний период года, т. е. имеет Сезонный характер.
Построенная нами модель Не учитывает фактор сезонности спроса и потому оказывается неадекватной. Вследствие этого, такая модель не может, в частности, использоваться для прогнозирования объема спроса в зависимости от величины совокупного располагаемого дохода.
Для коррекции моделей связи в подобных ситуациях часто привлекают искусственно построенные переменные — «Фиктивные переменные» («dummy» variables). В нашем случае в качестве такой дополнительной переменной можно взять, например, переменную ![]() , значение которой равно
, значение которой равно ![]() для первого и четвертого кварталов и равно
для первого и четвертого кварталов и равно ![]() для второго и третьего кварталов. Добавление такой переменной в качестве объясняющей позволяет учесть сезонные колебания спроса. Оценивание расширенной модели дает следующие результаты.
для второго и третьего кварталов. Добавление такой переменной в качестве объясняющей позволяет учесть сезонные колебания спроса. Оценивание расширенной модели дает следующие результаты.
|
Dependent Variable: SALES | ||||
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
Prob. |
|
C |
26.21787 |
3.152042 |
8.317742 |
0.0000 |
|
DPI |
0.112653 |
0.017847 |
6.312227 |
0.0000 |
|
DUMMY |
6.028524 |
0.539997 |
11.16399 |
0.0000 |
|
R-squared |
0.813644 |
Mean dependent var |
48.94571 | |
|
Adjusted R-squared |
0.803571 |
S. D. dependent var |
3.852032 | |
|
S. E. of regression |
1.707233 |
Akaike info criterion |
3.979663 | |
|
Sum squared resid |
107.8419 |
Schwarz criterion |
4.106329 | |
|
Log likelihood |
-76.59327 |
F-statistic |
80.77244 | |
|
Durbin-Watson stat |
1.452616 |
Prob (F-statistic) |
0.000000 | |
Оцененное значение ![]() коэффициента при переменной
коэффициента при переменной ![]() фактически означает, что спрос на лыжный инвентарь в течение первого и четвертого кварталов возрастает по сравнению со спросом в течение второго и четвертого кварталов в среднем примерно на
фактически означает, что спрос на лыжный инвентарь в течение первого и четвертого кварталов возрастает по сравнению со спросом в течение второго и четвертого кварталов в среднем примерно на ![]() Млн Долларов (в ценах 1972 г.). Следующий график иллюстрирует качество подобранной расширенной модели.
Млн Долларов (в ценах 1972 г.). Следующий график иллюстрирует качество подобранной расширенной модели.

На сей раз значение![]() для статистики критерия Бройша-Годфри равно
для статистики критерия Бройша-Годфри равно ![]() против прежнего значения
против прежнего значения ![]() , так что этот критерий теперь Не отвергает гипотезу независимости случайных ошибок
, так что этот критерий теперь Не отвергает гипотезу независимости случайных ошибок ![]() .
.
По-существу, мы подобрали две различные модели линейной связи между ![]() и
и ![]() :
:
Модель
![]()
Для весенне-летнего периода;
Модель
![]()
Для осенне-зимнего периода.
При этом, предельная склонность к закупке лыжного инвентаря в обеих моделях остается одинаковой и оценивается величиной ![]() .
.
Замечание. Вместо подбора отдельных моделей для осенне-зимнего и весенне-летнего периодов можно было бы заняться подбором отдельных моделей для каждого из четырех кварталов года. С этой целью в качестве дополнительных объясняющих переменных можно взять, например, переменные ![]() , принимающие значение
, принимающие значение ![]() , соответственно, в четвертом, первом и втором кварталах, и равные нулю в остальных кварталах. При оценивании такой расширенной модели для наших данных оказывается незначимым коэффициент при
, соответственно, в четвертом, первом и втором кварталах, и равные нулю в остальных кварталах. При оценивании такой расширенной модели для наших данных оказывается незначимым коэффициент при ![]() , что означает близость в среднем уровней продаж во втором и в третьем кварталах. Более того, оказываются близкими оценки коэффициентов при переменных
, что означает близость в среднем уровней продаж во втором и в третьем кварталах. Более того, оказываются близкими оценки коэффициентов при переменных ![]() и
и ![]() . Гипотеза о совпадении двух последних коэффициентов не отвергается, и в итоге мы возвращаемся к модели с одной фиктивной переменной
. Гипотеза о совпадении двух последних коэффициентов не отвергается, и в итоге мы возвращаемся к модели с одной фиктивной переменной ![]() , которую мы уже оценили ранее.
, которую мы уже оценили ранее.
Использование фиктивных переменных полезно при анализе Агрегированных (объединенных) данных, полученных при объединении наблюдений, относящихся к различным полам (мужчины и женщины), к различным возрастным, языковым и социальным группам, к различным периодам времени. В таких ситуациях модели, построенные по отдельным группам, могут существенно различаться, и тогда модель, построенная по объединенным данным, не учитывает этого различия. Привлечение фиктивных переменных позволяет оценить значимость такого различия и по результатам этой оценки остановиться на модели с агрегированными данными или на модели, в которой учитывается различие параметров связи для различных групп (периодов времени).
В качестве примера, попробуем построить модель связи между переменными ![]() и
и ![]() , которые в 15 наблюдениях имели следующие значения:
, которые в 15 наблюдениях имели следующие значения:
|
X |
Z |
X |
Z |
X |
Z |
|
1 |
1.257 |
6 |
0.865 |
11 |
1.804 |
|
2 |
1.812 |
7 |
1.930 |
12 |
1.956 |
|
3 |
3.641 |
8 |
2.944 |
13 |
3.134 |
|
4 |
4.401 |
9 |
4.316 |
14 |
4.649 |
|
5 |
5.561 |
10 |
5.323 |
15 |
4.559 |
Этим данным соответствует приведенная ниже диаграмма рассеяния;
Прямая на диаграмме соответствует подобранной модели связи
![]() ;
;
![]() - статистика для коэффициента при
- статистика для коэффициента при ![]() принимает значение
принимает значение ![]() , что дает
, что дает ![]() и ведет к неотвержению гипотезы о равенстве этого коэффициента нулю. Регрессия переменной
и ведет к неотвержению гипотезы о равенстве этого коэффициента нулю. Регрессия переменной ![]() на переменную
на переменную ![]() Признается незначимой.
Признается незначимой.
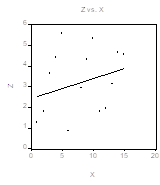
График указывает на наличие Трех режимов линейной связи между переменными ![]() И
И ![]() , соответствующим 5 первым, 5 центральным и 5 последним наблюдениям. Коэффициент при
, соответствующим 5 первым, 5 центральным и 5 последним наблюдениям. Коэффициент при ![]() кажется одинаковым для всех трех режимов, тогда как постоянные различаются.
кажется одинаковым для всех трех режимов, тогда как постоянные различаются.
В то же время, график остатков от подобранной модели связи явно указывает на неправильную спецификацию модели:

Чтобы учесть обнаруженное по графику остатков наличие трех режимов, привлечем в качестве дополнительных объясняющих переменных две фиктивные переменные: переменную ![]() , равную
, равную ![]() в Пяти Центральных наблюдениях и равную
в Пяти Центральных наблюдениях и равную ![]() в остальных наблюдениях, а также переменную
в остальных наблюдениях, а также переменную ![]() , равную
, равную ![]() в Пяти последних наблюдениях и равную
в Пяти последних наблюдениях и равную ![]() в остальных наблюдениях. Оценивание расширенной модели с участием этих дополнительных объясняющих переменных дает следующий результат:
в остальных наблюдениях. Оценивание расширенной модели с участием этих дополнительных объясняющих переменных дает следующий результат:
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
Prob. |
|
C |
0.264368 |
0.274073 |
0.964591 |
0.3555 |
|
X |
1.023398 |
0.070765 |
14.46185 |
0.0000 |
|
D2 |
-5.375960 |
0.430449 |
-12.48920 |
0.0000 |
|
D3 |
-10.34806 |
0.748910 |
-13.81749 |
0.0000 |
|
R-squared |
0.950286 |
Mean dependent var |
3.210213 | |
|
Durbin-Watson stat |
2.205754 |
Prob (F-statistic) |
0.000000 | |
На этот раз регрессия оказывается не только Статистически значимой, но и имеет очень высокую значимость; то же относится и к коэффициентам при переменных![]() ,
,![]() и
и ![]() . Высокая значимость двух последних коэффициентов подтверждает Значимое отличие констант в моделях линейной связи между переменными
. Высокая значимость двух последних коэффициентов подтверждает Значимое отличие констант в моделях линейной связи между переменными ![]() И
И ![]() .
.
В заключение обратимся опять к примеру, рассмотренному в параграфе 3.3. Мы обнаружили там, что модель линейной связи
![]()
Оказалась неудовлетворительной, поскольку анализ остатков от оцененной модели выявил гетероскедастичность и автокоррелированность ошибок и отличие распределения ошибок от нормального. Приведенные там график зависимости стандартизованных остатков ![]() от номера наблюдений и его вариант в виде зависимости от года наблюдения указывают на явную разницу в поведении остатков в первой части периода наблюдений (до 1972 года) и во второй его части (1973-1985 годы). Такое различие в поведении остатков свидетельствует о том, что в 1973 году произошел структурный сдвиг в экономической ситуации, связанный с мировым топливо-энергетическим кризисом, который изменил характер связи между рассматриваемыми макроэкономическими факторами. Последнее могло, например, выразиться в изменении значений параметров
от номера наблюдений и его вариант в виде зависимости от года наблюдения указывают на явную разницу в поведении остатков в первой части периода наблюдений (до 1972 года) и во второй его части (1973-1985 годы). Такое различие в поведении остатков свидетельствует о том, что в 1973 году произошел структурный сдвиг в экономической ситуации, связанный с мировым топливо-энергетическим кризисом, который изменил характер связи между рассматриваемыми макроэкономическими факторами. Последнее могло, например, выразиться в изменении значений параметров ![]() при переходе ко второй части периода наблюдений. Возможность такого изменения учитывает расширенная модель
при переходе ко второй части периода наблюдений. Возможность такого изменения учитывает расширенная модель
![]()
Здесь
![]() - фиктивная переменная, равная
- фиктивная переменная, равная ![]() для
для ![]() (что соответствует периоду с 1959 по 1972 год) и равная
(что соответствует периоду с 1959 по 1972 год) и равная ![]() для
для ![]() (что соответствует периоду с 1973 по 1985 год),
(что соответствует периоду с 1973 по 1985 год),
![]() - фиктивная переменная, равная
- фиктивная переменная, равная ![]() для
для ![]() и равная
и равная ![]() для
для ![]() ,
,
![]() - переменная, равная
- переменная, равная![]() для
для ![]() и равная
и равная ![]() для
для ![]() ,
,
![]() - переменная, равная
- переменная, равная ![]() для
для ![]() и равная
и равная ![]() для
для ![]() ,
,
![]() - переменная, равная
- переменная, равная ![]() для
для ![]() и равная
и равная ![]() для
для ![]() ,
,
![]() - переменная, равная
- переменная, равная ![]() для
для ![]() и равная
и равная ![]() для
для ![]() .
.
Заметим, что при этом
![]()
![]()
В рамках расширенной модели проверим гипотезу
![]()
Используя ![]() -критерий. Значению
-критерий. Значению ![]() -статистики
-статистики ![]() соответствует
соответствует ![]() -значение
-значение ![]() , так что гипотеза
, так что гипотеза ![]() отвергается, и это говорит об изменении хотя бы одного из параметров
отвергается, и это говорит об изменении хотя бы одного из параметров ![]() при переходе ко второй части периода наблюдений. Поскольку оценки параметров
при переходе ко второй части периода наблюдений. Поскольку оценки параметров ![]() и
и ![]() статистически незначимы (им соответствуют
статистически незначимы (им соответствуют ![]() -значения
-значения ![]() и
и ![]() ), проверим гипотезу о равенстве нулю обоих этих параметров. Получаемое
), проверим гипотезу о равенстве нулю обоих этих параметров. Получаемое ![]() -значение
-значение ![]() означает, что последняя гипотеза не отвергается, так что допуская изменение параметров модели при переходе ко второй части периода наблюдений, можно вообще отказаться от включения в модель переменной
означает, что последняя гипотеза не отвергается, так что допуская изменение параметров модели при переходе ко второй части периода наблюдений, можно вообще отказаться от включения в модель переменной ![]() и ограничиться моделью
и ограничиться моделью
![]()
Оценивание этой модели дает следующие результаты: ![]() ,
,
![]()
![]()
![]()
![]()
Гипотеза ![]() здесь отвергается
здесь отвергается ![]() , как и гипотеза
, как и гипотеза ![]() , так что структурный сдвиг затрагивает и постоянную и коэффициент при
, так что структурный сдвиг затрагивает и постоянную и коэффициент при ![]() .
.
Значение статистики Дарбина-Уотсона равно ![]() и не выявляет автокоррелированности ошибок. К тому же результату приводит и применение критерия Бройша-Годфри с
и не выявляет автокоррелированности ошибок. К тому же результату приводит и применение критерия Бройша-Годфри с ![]()
![]()
![]() . Критерий Уайта дает
. Критерий Уайта дает![]() , не выявляя гетероскедастичности, а критерий Жарка-Бера дает
, не выявляя гетероскедастичности, а критерий Жарка-Бера дает ![]() , не выявляя существенных отклонений распределения ошибок от нормального.
, не выявляя существенных отклонений распределения ошибок от нормального.
Вспомним, однако, про критерий Голдфелда-Квандта. Опять выделяя периоды с 1960 по 1969 год и с 1976 по 1985 год, получаем значение ![]() -статистики
-статистики ![]() , соответствующее
, соответствующее ![]() , так что на сей раз и этот критерий не обнаруживает существенной гетероскедастичности.
, так что на сей раз и этот критерий не обнаруживает существенной гетероскедастичности.
Тем самым, мы имеем основания принять в качестве возможной модели наблюдений, объясняющей изменения объема совокупного потребления на периоде с 1959 по 1985 год, оцененную модель
![]()
Эту модель можно также записать в виде
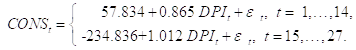
Соответственно последней форме записи такая модель называется Двухфазной линейной регрессией (Или Линейной моделью с переключением). Заметим, наконец, что допустив возможность изменения постоянной и коэффициента при ![]() при переходе ко второй части периода наблюдений, мы можем допустить при этом и изменение дисперсии ошибок, т. е. полагать, что
при переходе ко второй части периода наблюдений, мы можем допустить при этом и изменение дисперсии ошибок, т. е. полагать, что ![]() для
для ![]() и
и ![]() для
для ![]() . Оценки для
. Оценки для ![]() и
и ![]() в этом случае равны, соответственно,
в этом случае равны, соответственно, ![]() и
и ![]() .
.
| < Предыдущая | Следующая > |
|---|