3.4. Коррекция статистических выводов при наличии гетероскедастичности (неоднородности дисперсий ошибок)
Пример. Для исследования вопроса о зависимости количества руководящих работников от размера предприятия были собраны статистические данные по 27 промышленным предприятиям. Далее обозначено:
— численность персонала на I-М предприятии,
— количество руководителей на I-М предприятии.
Оцениваем линейную модель наблюдений
Регрессионный анализ дает следующие результаты: R2= 0.776 и
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
P-value. |
|
1 |
14.448 |
9.562 |
1.511 |
0.1433 |
|
X |
0.105 |
0.011 |
9.303 |
0.0000 |
Следующие два графика демонстрируют диаграмму рассеяния с подобранной прямой 
(левый график) и зависимость стандартизованных остатков 
от значений 
(правый график).
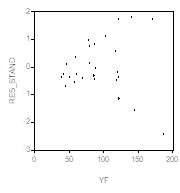
Похоже, что имеет место тенденция линейного возрастания абсолютных величин остатков с ростом 
, соответствующая наличию приближенной зависимости вида 
для дисперсий ошибок. Чтобы погасить такую неоднородность дисперсий, разделим обе части соотношения 
На :
Т. е. перейдем к модели наблюдений
Где
Если Действительно выполняется соотношение 
, то тогда в преобразованной модели
Т. е. неоднородность дисперсий ошибок преодолевается.
Результаты оценивания преобразованной модели:
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
P-value. |
|
1 |
0.121 |
0.009 |
13.445 |
0.0000 |
|
1/x |
3.803 |
4.570 |
0.832 |
0.4131 |
В исходных переменных это соответствует модели линейной связи
Отметим уменьшение оцененных стандартных ошибок оценок обоих параметров 
и
. Именно на эти значения следует опираться при построении доверительных интервалов для этих параметров. Средними точками этих интервалов будут, соответственно, 
и 
. Следующий график показывает характер зависимости стандартизованных остатков в преобразованной модели от 
.
На сей раз неоднородности дисперсий остатков (по крайней мере явной) Не обнаруживается.
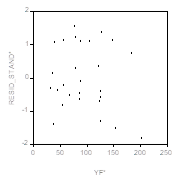
Рассмотрим внимательнее наши действия при оценивании преобразованной модели. Оценки коэффициентов, приведенные в последней таблице, получены применением метода наименьших квадратов к модели наблюдений Т. е. путем минимизации суммы квадратов
Которую, вспоминая, что обозначают переменные со звездочками, можно записать в виде
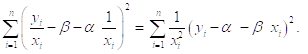
Обозначая теперь
Получаем, что задача минимизации суммы квадратов отклонений в преобразованной модели равносильна задаче минимизации Взвешенной суммы квадратов Отклонений в Исходной (непреобразованной) модели. Величина 
интерпретируется в этом контексте как Вес, приписываемый квадрату отклонения в 
- м наблюдении. Этот вес будет тем меньше, чем больше значение 
, которое в силу наших предположений пропорционально дисперсии случайной ошибки в -м наблюдении. Следовательно, чем больше дисперсия случайной ошибки 
, тем меньше вес, с которым входит квадрат отклонения в -м наблюдении в минимизируемую сумму.
Имея в виду, что оценивание преобразованной модели наблюдений сводится к минимизации суммы
Рассмотренный метод оценивания называют Взвешенным методом наименьших квадратов (хотя точнее его следовало бы называть Методом наименьших взвешенных квадратов).
Замечание. В некоторых руководствах по эконометрике и в некоторых пакетах статистического анализа данных (например, в пакете EVIEWS) используется несколько иное равносильное представление минимизируемой суммы квадратов в преобразованной модели наблюдений:
В этом случае вес приписывается Не квадрату отклонения, а Самому Отклонению 
Разумеется, в рассмотренном примере при таком определении веса последний будет равен
На это обстоятельство следует обратить внимание при спецификации весов в процедурах, реализующих взвешенный метод наименьших квадратов.
Обратим теперь внимание на то, в каком виде выдается информация о результатах применения взвешенного метода наименьших квадратов на примере пакета EVIEWS. При этом используем данные из рассмотренного выше примера. Согласно сказанному в Замечании, при обращении к процедуре оценивания взвешенным методом наименьших квадратов в условиях нашего примера мы специфицируем веса как 
.
Протокол оценивания имеет следующий вид:
|
Dependent Variable: Y | ||||
|
Method: Least Squares | ||||
|
Date: Time: | ||||
|
Sample: 1 27 | ||||
|
Included observations: 27 | ||||
|
Weighting series: 1/X | ||||
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
Prob. |
|
C |
3.803296 |
4.569745 |
0.832277 |
0.4131 |
|
X |
0.120990 |
0.008999 |
13.44540 |
0.0000 |
|
Weighted Statistics | ||||
|
R-squared |
0.026960 |
Mean dependent var |
74.04946 | |
|
Adjusted R-squared |
–0.011961 |
S. D. dependent var |
13.08103 | |
|
S. E. of regression |
13.15902 |
Akaike info criterion |
8.063280 | |
|
Sum squared resid |
4328.998 |
Schwarz criterion |
8.159268 | |
|
Log likelihood |
-106.8543 |
F-statistic |
180.7789 | |
|
Durbin-Watson stat |
2.272111 |
Prob (F-statistic) |
0.000000 | |
|
Unweighted Statistics | ||||
|
R-squared |
0.758034 |
Mean dependent var |
94.44444 | |
|
Adjusted R-squared |
0.748355 |
S. D. dependent var |
45.00712 | |
|
S. E. of regression |
22.57746 |
Sum squared resid |
12743.54 | |
|
Durbin-Watson stat |
2.444541 |
В этом протоколе приводятся значения двух видов статистик:
· Weighted Statistics (взвешенные статистики) — Это статистики, основанные на остатках, получаемых по взвешенным данным, т. е. на остатках 
в Преобразованной модели.
· Unweighted Statistics (невзвешенные статистики) — Это статистики, основанные на «остатках» 
т. е. на отклонениях наблюдаемых значений объясняемой переменной 
от значений, предсказываемых линейной моделью связи, в качестве параметров которой берутся их оценки 
полученные в Преобразованной модели.
Отметим весьма низкое (0.2696) значение коэффициента детерминации в преобразованной модели. Однако это обстоятельство не должно нас волновать — линейная связь в преобразованной модели Значима, о чем говорит весьма высокое значение 
-статистики, равное 180.7789, и соответствующее ему 
-значение 0.0000 (см. Weighted Statistics).
В конечном счете нас интересует значение 
, находящееся в части протокола, соответствующей невзвешенным статистикам, а это значение достаточно велико (0.7580).
Отметим еще, что приведенные в начале таблицы значения оценок параметров, их стандартных ошибок и 
-статистик, а также -значения соответствуют величинам, полученным на стадии оценивания Преобразованной модели.
Заметим, наконец, что значение 
, указанное в числе Невзвешенных статистик, отличается от значения 
, полученного нами при оценивании исходной (непреобразованной) модели наблюдений. Причина этого, разумеется, в том, что при вычислении значения 
использовались остатки
Где 
— оценки наименьших квадратов параметров исходной модели, полученные Без использования взвешивания отклонений.
Мы уже отмечали выше, что результатом неоднородности дисперсий случайных ошибок в модели наблюдений является Смещение оценок Дисперсий случайных величин 
. В то же время, наличие такого нарушения стандартных предположений Оставляет оценки Несмещенными. В связи с этим, один из методов коррекции статистических выводов при неоднородности дисперсий ошибок состоит в использовании Обычных оценок наименьших квадратов (OLS-оценок, Ordinary Least Squares estimates) 
коэффициентов 
вместе со Скорректированными на гетероскедастичность Оценками стандартных ошибок 
. Один из вариантов получения скорректированных на гетероскедастичность значений 
был предложен Уайтом (White) И реализован в ряде пакетов статистического анализа данных, в том числе и в пакете EVIEWS. При этом удовлетворительные свойства оценки Уайта гарантируются только при Большом количестве наблюдений. Мы не будем приводить здесь детали получения оценки Уайта, а просто воспользуемся пакетом EVIEWS для анализа данных из только что рассмотренного примера.
Пример. Используем данные из предыдущего примера, но применим для их анализа последнюю процедуру. Согласно этой процедуре, мы оцениваем Коэффициенты и
Обычным методом наименьших квадратов, так что в качестве оценок берутся значения 
и 
. В качестве же оценок Стандартных ошибок 
и 
вместо значений 
и 
, полученных выше при оценивании модели обычным методом наименьших квадратов, берем значения оценок Уайта 
и 
.
Бросающееся в глаза значительное различие оценок для параметра при применении двух рассмотренных методов (
и 
) в действительности не столь уж удивительно, поскольку оценки стандартной ошибки для
, полученные каждым из двух методов довольно высоки (
И 
, соответственно).
Избавиться от неоднородности дисперсий ошибок в ряде случаев позволяет Переход к логарифмам объясняемой переменной.
Пример. По данным, использованным в двух предыдущих примерах, оценим модель наблюдений
График зависимости стандартизованных остатков, полученных при оценивании этой модели, от предсказанных значений 
(левый график)
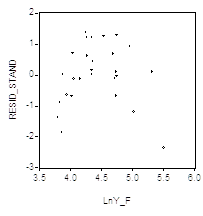
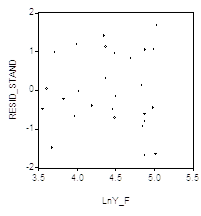
Указывает на неправильную спецификацию модели, связанную с возможным пропуском квадратичной составляющей . Оценивание расширенной модели наблюдений, включающей Дополнительную объясняющую переменную 
, приводит к остаткам, обнаруживающим существенно более удовлетворительное поведение (см. правый график). Результаты оценивания расширенной модели приведены в следующей таблице.
|
Variable |
Coefficient |
Std. Error |
T-Statistic |
P-value |
|
1 |
2.851 |
0.157 |
18.205 |
0.0000 |
|
X |
0.003 |
0.000399 |
7.803 |
0.0000 |
|
X2 |
-1.10E-06 |
2.24E-07 |
-4.925 |
0.0001 |
Таким образом, используя преобразования переменных, мы получили две альтернативные оцененные модели связи между переменными 
и 
:
и 
.
Первую из этих двух моделей можно предпочесть из соображений простоты интерпретации.
| < Предыдущая | Следующая > |
|---|
