2.12. Использование оцененной модели для прогнозирования

Пусть мы имеем модель наблюдений в виде модели простой линейной регрессии

И хотим дать прогноз, каким будет значение объясняемой переменной при некотором выбранном (фиксированном) значении объясняющей переменной , если мы будем продолжать наблюдения.

Мы умеем оценивать коэффициенты и методом наименьших квадратов, и естественно использовать для целей прогнозирования получаемую в результате такого оценивания (подобранную) модель линейной связи

Что приводит к Прогнозируемому значению Объясняемой переменной, равному

Вопрос только в том, Сколь надежным является выбор такого значения в качестве прогнозного. И здесь надо иметь в виду следующее.

Поскольку мы используем для прогноза оценки, полученные, исходя из модели наблюдений то для того, чтобы этот прогноз был осмысленным, нам по необходимости приходится предполагать, что структура модели наблюдений и ее параметры Не изменятся при переходе к новому наблюдению, так что соответствующее значение должно описываться Тем же линейным соотношением . В таком случае, мы по-существу имеем дело с расширенной линейной моделью с наблюдениями, в которой дополнительное наблюдение удовлетворяет соотношению

При этом, случайная величина должна иметь То же распределение, что и случайные величины и должна образовывать вместе с ними множество случайных величин, независимых в совокупности.

Итак, мы договорились, что в расширенной модели

Выбирая в качестве прогноза для значение Мы тем самым допускаем Ошибку прогноза, равную

Поскольку вычисленные оценки являются (как мы уже выяснили выше) реализациями случайных величин, наблюдаемая ошибка прогноза также является реализацией случайной величины и включает два источника неопределенности:

· неопределенность, связанную с отклонением вычисленных значений случайных величин От истинных значений параметров ;

· неопределенность, связанную со случайной ошибкой в- м наблюдении.

При наших Стандартных предположениях о линейной модели наблюдений ошибка прогноза является Случайной величиной , имеющей математическое ожидание

(Мы использовали здесь справедливые при выполнении стандартных предположений соотношения )

Точность прогноза характеризуется Дисперсией ошибки прогноза

Здесь использован тот факт, что сумма Неслучайна (хотя ее точное значение и не известно). Далее, из предположенной независимости случайных ошибок и вытекает независимость случайных величин (эта величина зависит от случайных ошибок ) и (последняя Не зависит от случайных ошибок ). В силу же независимости и ,

(использовано правило сложения дисперсий). Остается заметить, что

Где, как обычно, (Мы не будем выводить эту формулу.) Таким образом,

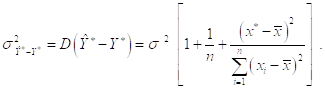
Если случайные ошибки имеют Нормальное распределение, то тогда случайные величины и

Также имеют нормальные распределения. При этом, ошибка прогноза имеет нормальное распределение с нулевым математическим ожиданием и дисперсией, вычисляемой по последней формуле.

Разделив разность на квадратный корень из ее дисперсии, получаем случайную величину

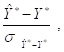
Имеющую Стандартное нормальное распределение . Заменяя в правой части выражения для Неизвестное значение его несмещенной оценкой , получаем оценку дисперсии в виде

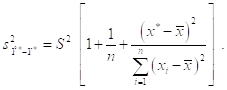
Заменяя, наконец, в знаменателе отношения, имеющего стандартное нормальное распределение, неизвестное значение его оценкой , приходим к -статистике (-отношению)

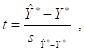
Имеющей При выполнении сделанных предположений о модели наблюдений -распределение Стьюдента с Степенями свободы.

Последний факт дает возможность построения -процентного доверительного интервала для значения

А именно,

На основании которого получаем -процентный доверительный интервал для :

— здесь мы использовали то, что в силу симметрии распределения Стьюдента, .

Заметим, что при заданных значениях (по которым строится прогноз) доверительный интервал для будет Тем длинее, чем больше значение . Последнее же равно при и возрастает с ростом . Это означает, что длина доверительного интервала Возрастает при удалении значения , при котором строится прогноз, от среднего арифметического значений .

Таким образом, прогнозы для значений , далеко отстоящих от , становятся менее определенными, поскольку длина соответствующих доверительных интервалов для значений объясняемой переменной возрастает.

Пример. Для данных о размерах совокупного располагаемого дохода и совокупных расходах на личное потребление в США в период с 1970 по 1979 год (в млрд. долларов, в ценах 1972 года), оцененная модель линейной связи имеет вид .

Представим себе, что мы находимся в 1979 году и ожидаем увеличения в 1980 году совокупного располагаемого дохода (в тех же ценах) до млрд. долларов. Тогда прогнозируемый по подобранной модели объем совокупных расходов на личное потребление в 1980 году равен

Так что если выбрать уровень доверия , то

И доверительный интервал для соответствующего значения имеет вид

Т. е.

Или

Заметим, что интервал достаточно широк и его нижняя граница допускает даже возможность некоторого снижения уровня потребления по сравнению с предыдущим годом.

В действительности, в 1980 г. совокупный располагаемый доход достиг 1021 млрд. долларов, а совокупное потребление — 931.8 млрд. долларов. Тем самым, ошибка прогноза составила

Если бы мы исходили при прогнозе из Действительного значения , а не из , то прогнозируемое значение для равнялось бы 931.94 и ошибка прогноза составила всего лишь

Проиллюстрируем, наконец, как изменяется в этом примере длина 95%-доверительных интервалов в интервале наблюдавшихся значений объясняющей переменной . На графике приведены отклонения нижней и верхней границ таких интервалов от центра интервала:

В случае модели Множественной линейной регрессии

Точечный прогноз значения соответствующего Фиксированному набору значений объясняющих переменных, дается формулой

Где — оценки наименьших квадратов параметров. Интервальный прогноз Имеет вид

Где

— оценка дисперсии ошибки прогноза, а - несмещенная оценка дисперсии Случайных ошибок.

< Предыдущая		Следующая >