2.05. Нормальная множественная регрессия: доверительные интервалы . для коэффициентов

Рассматривая нормальную модель линейной множественной регрессии

С ~ I. i. d. , мы установили, что оценка наименьших квадратов неизвестного истинного значения коэффициента при — ой объясняющей переменной имеет нормальное распределение, причем

Рассмотрим теперь случайную величину

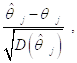
Получаемую путем вычитания из случайной величины ее математического ожидания и деления полученной разности на корень из дисперсии (т. е. путем Центрирования и Нормирования Случайной величины ). При совершении этих двух действий мы не выходим из семейства нормальных случайных величин, получая опять же Нормальную случайную величину, но только уже с другими математическим ожиданием и дисперсией. Используя упомянутые ранее свойства математического ожидания и дисперсии, находим:

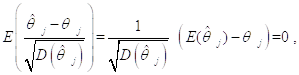
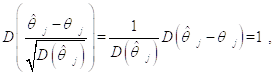
Так что

~

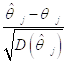Иными словами, в результате центрирования и нормирования случайной величины мы получили случайную величину, имеющую Стандартное нормальное распределение, т. е. Нормальное распределение с нулевым математическим ожиданием и единичной дисперсией. Функцию распределения и функцию плотности распределения такой случайной величины обозначают, соответственно, как и :

Для каждого значения , определим символом число, для которого , так что если случайная величина имеет стандартное нормальное распределение, то тогда

Такое число называется Квантилью уровня p Стандартного нормального распределения.

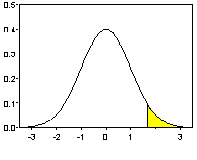
Заштрихованная площадь под графиком плотности стандартного нормального распределения находится Правее квантили уровня ;

Эта квантиль равна . Поэтому площадь под кривой, лежащая Левее точки , равна , а Заштрихованная площадь равна . Последняя величина есть вероятность того, что случайная величина , имеющая стандартное нормальное распределение, примет значение, Превышающее .

Если мы возьмем какое-нибудь число в пределах от до , , и выделим интервал

То получим следующую картину:

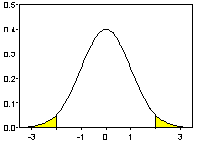
Из симметрии функции плотности нормального распределения вытекает равенство площадей областей, заштрихованных на последнем рисунке. Но площадь правой заштрихованной области равна ; следовательно, такова же и площадь левой заштрихованной области. Это, в частности, означает, что вероятность того, что случайная величина примет значение, не превышающее , равна , так что

Часть площади под кривой стандартной нормальной плотности, лежащая в Пределах выделенного интервала, меньше единицы на сумму площадей заштрихованных областей («Хвостов»), т. е. равна

Эта величина равна Вероятности того, что случайная величина , имеющая Стандартное нормальное распределение, примет значение в пределах указанного интервала[2]:

Но ранее мы установили, что стандартное нормальное распределение имеет случайная величина

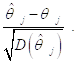
Поэтому для этой случайной величины справедливо соотношение

Так что с вероятностью, равной , выполняется двойное неравенство

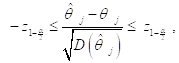
Т. е.

Иными словами, С вероятностью, равной 1-a, Случайный интервал

Накрывает истинное значение коэффициента Q j. Такой интервал называется Доверительным интервалом для Q j с уровнем доверия (доверительной вероятностью) 1-a, Или (1-a)-Доверительным интервалом, Или 100(1-a)-Процентным доверительным интервалом для Q j.

Последний рисунок был получен при значении A = 0.05. Поэтому площади заштрихованных областей («Хвосты») равны 0.025, сумма этих площадей равна 0.05 , и площадь области под кривой в пределах интервалаРавна 1-0.05 = 0.95. Остается заметить, что

Так что случайный интервал

Является 95%-доверительным интервалом для Q j. Его Длина

Пропорциональна — Среднеквадратической ошибке (среднеквадратическому отклонению) Оценки коэффициента Q j.

Хотелось бы, конечно, прямо сейчас построить доверительные интервалы для коэффициентов линейной модели по каким-нибудь реальным статистическим данным. Однако этому препятствует то обстоятельство, что в выражения для дисперсий

Входит Не известное нам Значение S 2.

[1] В литературе по эконометрике математическое ожидание случайной величины X Обозначают иногда символом M(X), а для дисперсии случайной величины X Используют также обозначения Var(X) и V(X).

[2] Заметим, что в этом и других подобных выражениях знак £ можно свободно заменять знаком < , а знак ³ знаком > (и обратно), поскольку мы Всегда предполагаем существование функции плотности распределений рассматриваемых случайных величин.

< Предыдущая		Следующая >