2.04. Нормальные линейные модели с . несколькими объясняющими переменными
Начиная с этого момента, мы будем предполагать, что
(1) Модель наблюдений имеет вид
![]()
Где ![]() - значение объясняемой переменной в
- значение объясняемой переменной в ![]() -м наблюдении;
-м наблюдении;
![]() - известное значение
- известное значение![]() -ой объясняющей переменной в
-ой объясняющей переменной в ![]() -м наблюдении;
-м наблюдении;
![]() - неизвестный коэффициент при
- неизвестный коэффициент при![]() -ой объясняющей переменной;
-ой объясняющей переменной;
![]() - случайная составляющая (“ошибка“) в
- случайная составляющая (“ошибка“) в ![]() -м наблюдении.
-м наблюдении.
(2) ![]() - Случайные величины, Независимые в совокупности, имеющие Одинаковое нормальное распределение N (0,S2) с нулевым математическим ожиданием и дисперсией
- Случайные величины, Независимые в совокупности, имеющие Одинаковое нормальное распределение N (0,S2) с нулевым математическим ожиданием и дисперсией ![]()
(3) Если не оговорено противное, то в число объясняющих переменных Включается переменная, тождественно равная единице, которая объявляется первой Объясняющей переменной, так что
![]()
При сделанных предположениях ![]() являются Наблюдаемыми значениями Нормально распределенных случайных величин
являются Наблюдаемыми значениями Нормально распределенных случайных величин ![]() , Которые Независимы в совокупности и для которых
, Которые Независимы в совокупности и для которых
![]()
Так что
![]() ~
~![]()
В отличие от ![]() , Случайные величины
, Случайные величины ![]() имеют распределения, Отличающиеся сдвигами.
имеют распределения, Отличающиеся сдвигами.
Определенную указанным образом модель наблюдений мы будем называть Нормальной линейной моделью С P Объясняющими переменными. Иначе ее еще называют Нормальной линейной моделью множественной регрессии переменной y на переменные x1, ... , Xp . Термин “множественная” указывает на использование в правой части модели наблюдений Двух и более объясняющих переменных, отличных от постоянной. Термин “регрессия” имеет определенные исторические корни и используется лишь в силу традиции.
Оценивание Неизвестных коэффициентов модели методом наименьших квадратов Состоит в минимизации по всем возможным значениям ![]() суммы квадратов
суммы квадратов
![]()
Минимум этой суммы достигается при некотором наборе значений коэффициентов
![]()
Так что
![]()
Это минимальное значение мы опять обозначаем RSS , так что
![]()
И называем Остаточной суммой квадратов.
Коэффициент детерминации R2 Определяется как
![]()
Где
![]()
Обозначая
![]()
(Подобранные - fitted- значения объясняющей переменной по оцененной линейной модели связи), и определяя остаток (Residual) От i-го наблюдения как
![]()
Мы получаем:
![]()
Обозначая
![]()
- Объясненная моделью (Explained) сумма квадратов, Или Регрессионная сумма квадратов, мы так же, как и в случае Простой линейной регрессии с ![]() , имеем разложение
, имеем разложение
![]()
Так что
![]()
И опять, это разложение справедливо только При наличии постоянной составляющей в модели линейной связи. При этом, также, здесь
![]()
Т. е. коэффициент детерминации равен квадрату выборочного коэффициента корреляции ![]() между переменными
между переменными ![]() и
и ![]() . Последний называется Множественным коэффициентом корреляции (Multiple-R).
. Последний называется Множественным коэффициентом корреляции (Multiple-R).
Для поиска значений ![]() , Минимизирующих сумму
, Минимизирующих сумму
![]()
Следует приравнять нулю частные производные этой суммы (как функции от ![]() ) По каждому из аргументов
) По каждому из аргументов ![]() . В результате получаем Систему нормальных уравнений
. В результате получаем Систему нормальных уравнений
![]()
![]()
![]()
![]()
Или
![]()
![]()
![]()
![]()
Это система ![]() линейных уравнений с
линейных уравнений с ![]() неизвестными
неизвестными ![]() . Ее можно решать или методом подстановки или по правилу Крамера с использованием соответствующих определителей. В векторно-матричной форме эта система имеет вид
. Ее можно решать или методом подстановки или по правилу Крамера с использованием соответствующих определителей. В векторно-матричной форме эта система имеет вид
![]()
Где
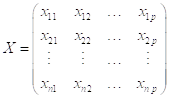
- матрица значений ![]() объясняющих переменных в
объясняющих переменных в ![]() наблюдениях;
наблюдениях;
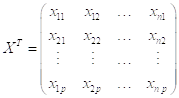
- транспонированная матрица;
 и
и 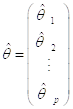
Соответственно, вектор-столбец значений объясняемой переменной в ![]() наблюдениях и вектор-столбец оценок
наблюдениях и вектор-столбец оценок ![]() неизвестных коэффициентов. Система нормальных уравнений Имеет единственное решение, если выполнено условие
неизвестных коэффициентов. Система нормальных уравнений Имеет единственное решение, если выполнено условие
(4) Матрица XTX невырождена, Т. е. ее Определитель отличен от нуля:
![]()
Которое можно заменить условием
(4’) Столбцы матрицы X линейно независимы.
При выполнении этого условия матрица ![]() (размера
(размера ![]() ) имеет обратную к ней матрицу
) имеет обратную к ней матрицу ![]() . Умножая в таком случае обе части последнего уравнения слева на матрицу
. Умножая в таком случае обе части последнего уравнения слева на матрицу ![]() , находим искомое решение системы нормальных уравнений:
, находим искомое решение системы нормальных уравнений:
![]()
Введем дополнительные обозначения
 ,
, 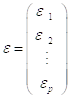 ,
, 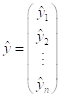 ,
, 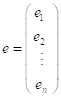 .
.
Тогда модель наблюдений
![]()
Можно представить в матрично-векторной форме
![]()
Вектор подобранных значений имеет вид
![]()
И вектор остатков равен
![]()
Определяющим для всего последующего является то обстоятельство, что в нормальной линейной модели с несколькими объясняющими переменными Оценки ![]() Коэффициентов
Коэффициентов ![]() как случайные величины имеют Нормальные распределения (хотя эти случайные величины уже не являются независимыми в совокупности).
как случайные величины имеют Нормальные распределения (хотя эти случайные величины уже не являются независимыми в совокупности).
Действительно, поскольку ![]() , то оценки
, то оценки ![]() являются Линейными комбинациями значений
являются Линейными комбинациями значений ![]() , Т. е. имеют вид
, Т. е. имеют вид
![]()
Где ![]() - коэффициенты, определяемые значениями объясняющих переменных. Поскольку же у нас
- коэффициенты, определяемые значениями объясняющих переменных. Поскольку же у нас ![]() - Наблюдаемые значения случайных величин
- Наблюдаемые значения случайных величин ![]() , то
, то ![]() является Наблюдаемым значением случайной величины
является Наблюдаемым значением случайной величины ![]() которую мы также будем обозначать
которую мы также будем обозначать ![]() :
:
Ранее мы выяснили, что при наших предположениях
![]() ~
~![]()
Поэтому случайные величины ![]() также будут нормальными как линейные комбинации независимых нормально распределенных случайных величин.
также будут нормальными как линейные комбинации независимых нормально распределенных случайных величин.
Можно показать, что математическое ожидание случайной величины![]() равно
равно
![]()
(![]() является Несмещенной оценкой Истинного значения коэффициента
является Несмещенной оценкой Истинного значения коэффициента ![]() ), а дисперсия этой случайной величины равна
), а дисперсия этой случайной величины равна ![]() -му диагональному элементу матрицы
-му диагональному элементу матрицы ![]() :
:
![]()
Рассмотренная ранее модель простой линейной регрессии
![]()
Вкладывается в модель множественной линейной регрессии с ![]() :
:
 ,
, 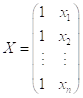 ,
, ![]() ,
, 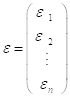 .
.
Матрица ![]() имеет вид
имеет вид
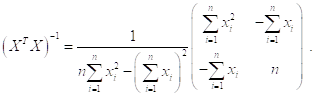
Учитывая, что
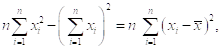
Находим:

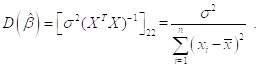
| < Предыдущая | Следующая > |
|---|