1.05. «обратная» модель прямолинейной связи

Пусть наша задача состоит в оценивании модели прямолинейной связи между некоторыми переменными и на основе наблюдений N Пар значений этих переменных. Мы уже рассмотрели вопрос об оценивании параметров такой связи, исходя из модели наблюдений . Что изменится, если мы будем исходить из «обратной» модели ?

Пусть — оценки параметров и в модели наблюдений , а — оценки параметров в модели наблюдений . Тогда

Т. е.

Или

В то же время, по первой модели наблюдений мы получаем наилучшую прямую

А по второй — прямую

Первую прямую мы можем записать в виде

Сравнивая коэффициенты при в двух последних уравнениях, находим, что эти коэффициенты равны В том и только в том случае, когда выполнено соотношение

Т. е.

Или, с учетом предыдущего, когда.

Что касается отрезков на осях, то они будут совпадать тогда и только тогда, когда

Или

Но

Так что

При получаем

В то же время,

Так что при совпадают и отрезки на осях, т. е. наилучшая прямая Одна и та же при обеих моделях наблюдений, и это есть прямая, на которой расположены Все наблюдаемые точки

Иными словами, наилучшие прямые, построенные по двум альтернативным моделям, совпадают в том и только в том случае, когда Все точки , расположены на одной прямой (так что ); при этом, . В противном случае,И подобранные «наилучшие» прямые имеют Разные угловые коэффициенты.

Кстати, в рассмотренном нами примере с уровнями безработицы, диаграмма рассеяния с Переставленными осями (соответствующими модели наблюдений ) имеет вид

Рис. 5

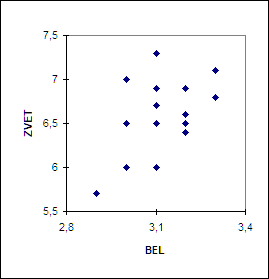
Количество точек с совпадающими знаками отклонений координат от средних значений равно 10 (4+ 6, с учетом совпадений), а число точек с противоположными знаками отклонений координат от средних значений равно 7 (4+3, с учетом совпадений). Соответственно, «облако точек» имеет некоторую вытянутость вдоль наклонной прямой, проведенной через «центр» облака. «Наилучшая» прямая имеет вид

Коэффициент детерминации равен

Произведение угловых коэффициентов 0.125265 и 1.695402 наилучших прямых в «прямой» и «обратной» моделях наблюдений равно 0.212374 и Совпадает со значением R2.

Отметим, что несовпадение наилучших прямых, конечно, связано с тем, что в этих двух альтернативных моделях наблюдений мы минимизировали Различные суммы квадратов: в «прямой» модели мы минимизировали сумму квадратов отклонений точек от подбираемой прямой в направлении, параллельном оси , а во втором — в направлении, параллельном оси .

< Предыдущая		Следующая >