1.04. Свойства выборочной ковариации, выборочной дисперсии и выборочного коэффициента корреляции
Вернемся теперь к определению выборочной ковариации и отметим некоторые ее свойства.
Пусть ![]() — Некоторая постоянная, а
— Некоторая постоянная, а ![]() — Переменные, принимающие в
— Переменные, принимающие в ![]() - М наблюдении значения
- М наблюдении значения ![]() ,
, ![]() (N — Количество наблюдений). Тогда
(N — Количество наблюдений). Тогда ![]() можно рассматривать как переменную, значения которой в
можно рассматривать как переменную, значения которой в ![]() - м наблюдении
- м наблюдении ![]() равно
равно ![]() , и
, и
![]()
Так что
![]()
Далее, очевидно, что
![]()
И что
![]()
Кроме того,
![]()
Так что
![]()
Наконец,
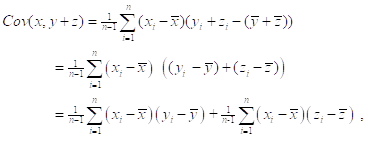
Так что
![]()
На основе этих свойств, в частности, находим, что
![]()
(постоянная не обладает изменчивостью),
![]()
(при изменений единицы измерения переменной в ![]() раз, во столько же раз изменяется и величина стандартного отклонения этой переменной),
раз, во столько же раз изменяется и величина стандартного отклонения этой переменной),
![]()
(сдвиг начала отсчета не влияет на изменчивость переменной).
Наконец,
![]()
Т. е.
![]()
(дисперсия суммы двух переменных отличается от суммы дисперсий этих переменных на величину, равную удвоенному значению ковариации между этими переменными).
Что касается выборочного коэффициента корреляции ![]() , то если Изменяются начало отсчета и единица измерения, скажем, переменной
, то если Изменяются начало отсчета и единица измерения, скажем, переменной ![]() , так что вместо значений
, так что вместо значений ![]() мы получаем значения
мы получаем значения
![]()
Переменной ![]() , то тогда
, то тогда
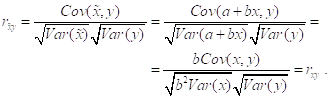
Иными словами, выборочный коэффициент корреляции ![]() , инвариантен Относительно выбора единиц измерения и начала отсчета переменных
, инвариантен Относительно выбора единиц измерения и начала отсчета переменных ![]() и
и ![]() .
.
В то же время, этого нельзя сказать об оценке ![]() коэффициента
коэффициента ![]() В модели наблюдений
В модели наблюдений ![]() . Действительно, если, скажем, мы переходим к новой единице измерения переменной
. Действительно, если, скажем, мы переходим к новой единице измерения переменной ![]() , так что вместо значений
, так что вместо значений ![]() наблюдаются значения переменной
наблюдаются значения переменной ![]() , то тогда оценка
, то тогда оценка![]() коэффициента
коэффициента ![]() в модели наблюдений
в модели наблюдений ![]() равна
равна
![]()
Таким образом, изменяя единицу измерения переменной ![]() (или переменной
(или переменной ![]() ), мы можем получать существенно различные значения
), мы можем получать существенно различные значения ![]() , от сколь угодно малых до сколь угодно больших. (Желательно выбирать единицы измерения таким образом, чтобы сравниваемые переменные имели одинаковый порядок.) Близость значений
, от сколь угодно малых до сколь угодно больших. (Желательно выбирать единицы измерения таким образом, чтобы сравниваемые переменные имели одинаковый порядок.) Близость значений ![]() к нулю всегда должна интерпретироваться с оглядкой на используемые единицы измерения переменных
к нулю всегда должна интерпретироваться с оглядкой на используемые единицы измерения переменных ![]() и
и ![]() .
.
Отметим, в этой связи, полезное представление ![]() в виде
в виде
![]()
Действительно,
![]()
Откуда и вытекает указанное представление. Из этого представления получаем, в частности, что при Var (X) = Var (Y) имеет место равенство ![]() , И тогда выраженность линейной связи между
, И тогда выраженность линейной связи между ![]() и
и ![]() непосредственно отражается в близости значения
непосредственно отражается в близости значения ![]() к
к ![]() или
или ![]() .
.
Рассмотрим теперь коэффициент корреляции ![]() между переменными
между переменными ![]() и
и ![]() , где
, где ![]() , а
, а ![]() и
и ![]() — оценки наименьших квадратов параметров
— оценки наименьших квадратов параметров ![]() и
и ![]() гипотетической линейной связи между переменными
гипотетической линейной связи между переменными ![]() и
и ![]() . Замечая, что
. Замечая, что ![]() (т. к.
(т. к. ![]() по определению), находим:
по определению), находим:
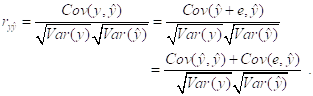
Но ранее мы уже получили (при выводе разложения для ![]() ) соотношение
) соотношение
![]()
Которое, с учетом соотношения ![]() , приводит к равенству
, приводит к равенству
![]()
![]()
Левая часть которого есть не что иное как
![]()
Следовательно,
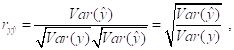
Так что
![]()
Последнее соотношение показывает, что коэффициент детерминации равен квадрату коэффициента корреляции между переменными ![]() и
и ![]() , так что при достаточно сильно выраженной линейной связи между переменными
, так что при достаточно сильно выраженной линейной связи между переменными ![]() и
и ![]() , что соответствует значению
, что соответствует значению ![]() , близкому к
, близкому к ![]() , оказывается близким к
, оказывается близким к ![]() и коэффициент корреляции между переменными
и коэффициент корреляции между переменными ![]() и
и ![]() .
.
По причинам, которые будут ясны из дальнейшего рассмотрения, ![]() называют Множественным коэффициентом корреляции (Multiple-R, Множественный-R).
называют Множественным коэффициентом корреляции (Multiple-R, Множественный-R).
Отметим также, что переменная ![]() измеряется В тех же единицах, что и переменная
измеряется В тех же единицах, что и переменная ![]() , и при изменении масштаба измерения переменной
, и при изменении масштаба измерения переменной ![]() значение
значение ![]() не изменяется. Отсюда вытекает, что коэффициент детерминации R2 инвариантен Относительно изменения масштаба и начала отсчета переменных
не изменяется. Отсюда вытекает, что коэффициент детерминации R2 инвариантен Относительно изменения масштаба и начала отсчета переменных ![]() и
и ![]() .
.
Заметим, наконец, что
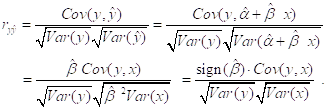
(здесь sign(z)=-1 для z<0, sign(z)=0 для z=0, sign(z)=1 для z>0)
Поскольку же
![]()
То ![]() и
и
![]()
Так что
![]()
И мы можем установить значение R2 Еще До построения модели линейной связи.
Замечание
Если ![]() , то
, то ![]() и
и ![]() ; если
; если ![]() , то
, то ![]() и
и ![]() , так что Всегда
, так что Всегда ![]()
| < Предыдущая | Следующая > |
|---|