1.06. Пропорциональная связь между переменными

Хотя на практике не рекомендуется отказываться от включения свободного члена в уравнение подбираемой прямолинейной связи, если только его отсутствие не обосновывается надежной теорией (как в физике — закон Ома), мы все же иногда сталкиваемся с необходимостью подбора прямой, проходящей через начало координат. Позднее мы приведем соответствующие примеры.

Итак, пусть мы имеем наблюдения , и предполагаем, что гипотетическая линейная связь между переменными и имеет вид

(Пропорциональная связь между переменными), так что ей соответствует модель наблюдений

.

Применение метода наименьших квадратов в этой ситуации сводится к минимизации суммы квадратов невязок

По всем возможным значениям . Последняя сумма квадратов является функцией Единственной переменной (при известных значениях ), и точка минимума этой функции легко находится. Для этого мы приравниваем нулю производную по :

(нормальное уравнение)

Откуда получаем:

Или

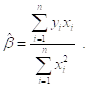
Отсюда видно, что при таком подборе

И точка уже Не лежит, как правило, на подобранной прямой

Более того, в такой ситуации

Где

И поэтому использовать для вычисления коэффициента детерминации выражение

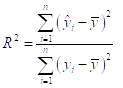
Не имеет смысла. В этой связи полезно рассмотреть следующий искусственный пример.

Пример

Пусть переменные и принимают в четырех наблюдениях значения, приведенные в следующей таблице

I	1	2	3	4
Xi	10	3	–10	-3
Yi	11	3	-9	-3

Соответствующей диаграмме рассеяния

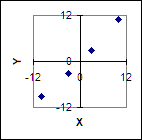
И мы предполагаем Пропорциональную связь между этими переменными, что соответствует модели наблюдений Для этих данных

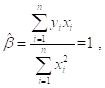
Так что При этом,

RSS = (11—10)2 + (3-3)2+ (-9+10)2+ (-3+3)2 = 2,

TSS = (11-0.5)2+ (3-0.5)2+ (-9-0.5)2+ (-3-0.5)2 = 219,

ESS = (10-0.5)2+ (3-0.5)2+ (-10-0.5)2+ (-3-0.5)2 = 219,

Так что здесь , и вычисление по формуле

Приводит к значению . Но последнее возможно только если все точки лежат на одной прямой, а у нас это не так. Заметим также, что в этом примере сумма остатков , что невозможно в модели с включением в правую часть постоянной составляющей.

Можно, конечно, попытаться справиться с возникающим при оценивании модели без постоянной составляющей затруднением, попросту игнорируя нарушение соотношения и определяя коэффициент детерминации соотношением

,

И именно такое значение приводится в протоколах некоторых пакетов программ анализа статистических данных, например пакета ECONOMETRIC VIEWS (TSP). Для нашего иллюстративного примера с четырьмя наблюдениями использование последнего приводит к значению , которое не противоречит интуиции и представляется разумным. Однако, к сожалению, и такой подход к определению коэффициента детерминации не решает проблемы, поскольку, в принципе, при оценивании модели без постоянной составляющей возможны ситуации, когда , что приводит к Отрицательным значениям .

Пример

Пусть переменные и принимают в четырех наблюдениях значения, приведенные в следующей таблице

I	1	2	3	4
Xi	0	0.2	0.4	3
Yi	0.5	0.8	1.2	2

Что соответствует диаграмме рассеяния

И мы предполагаем пропорциональную связь между этими переменными, что соответствует модели наблюдений Для этих данных . При этом, , , и вычисление по формуле приводит к Отрицательному значению

Преодолеть возникающие затруднения можно, если определить в модели наблюдений без постоянной составляющей формулой

,

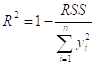В которой используется сумма квадратов Нецентрированных значений переменной (отклонений значений переменной от «нулевого уровня»). При таком определении, неотрицательность коэффициента Гарантируется наличием соотношения

Которое отражает Геометрическую сущность метода наименьших квадратов (аналог знаменитой теоремы Пифагора для многомерного простанства) и выполняется Как для модели без постоянной составляющей, так и для модели с наличием постоянной составляющей в правой части модели наблюдений. Деля обе части последнего равенства на приходим к соотношению

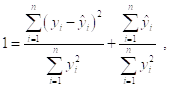
Из которого непосредственно следует, что

(Доказать заявленное равенство не сложно. Действительно,

Но

..

(см. нормальное уравнение), что и приводит к искомому результату.)

В последнем примере использование определения с Не центрированными Дает .

< Предыдущая		Следующая >