Глава 08. Отношения
Упорядоченные пары
Если А и B — Объекты, то через (А, B) обозначим Упорядоченную пару. Равенство Упорядоченных пар определяется следующим образом:
(А, B) = (С, D) Û а = C & B = D.
Вообще говоря, (А, b) ¹ (B, а).
Замечание
Упорядоченные пары можно рассматривать как множества, если определить их так:
(А, B) = {А,{А, b}}.
Таким образом, понятие упорядоченной пары не выводит рассмотрение за пределы теории множеств, но независимое определение технически удобнее.
Прямое произведение множеств
Пусть A И B — два множества. Прямым (декартовым) произведением Двух множеств А И В Называется множество упорядоченных пар, в котором первый элемент каждой пары принадлежит А, А второй принадлежит В:
А ´ В = {(А, B) | А ![]() А & B
А & B ![]() В}.
В}.
Степенью Множества А Называется его прямое произведение самого на себя. Обозначение:
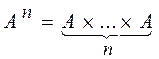
Соответственно, А1 = А, А2 = А ´ А И вообще АN = А ´ AN-1
ТЕОРЕМА |А ´ В| = |А| |В|.
СЛЕДСТВИЕ |Ап| = |А|п.
Отношения
Пусть А И В — Два множества. (Бинарным) отношением (или предикатом) R Из множества А В множество В Называется подмножество прямого произведения А И В:
R ![]() А ´ B.
А ´ B.
Для бинарных отношений обычно используется Инфиксная Форма записи:
АRb = (A, B) ![]()
![]()
Если А = В, То говорят, что R Есть отношение На множестве А.
Пример
Пусть задан универсум U. Тогда ![]() (принадлежность) — отношение из множества U В множество 2U, а
(принадлежность) — отношение из множества U В множество 2U, а ![]() (включение) и = (равенство) — отношения на 2U. Хорошо известны отношения =, <, <, >, >,
(включение) и = (равенство) — отношения на 2U. Хорошо известны отношения =, <, <, >, >, ![]() , определенные на множестве чисел.
, определенные на множестве чисел.
Пусть R Есть отношение на A: R ![]() А ´ A, A, B
А ´ A, A, B ![]() А. Введем следующие понятия
А. Введем следующие понятия
Обратное Отношение: R-1 = {(А, B) | (B, а) R}.
Дополнение Отношения: ![]() = {(А, B) | (A, B) R}.
= {(А, B) | (A, B) R}.
Тождественное Отношение: I = {(А, а) | а ![]() А}.
А}.
Универсальное Отношение: U = {(А, B) | а ![]() А & B
А & B ![]() А}.
А}.
Введем обобщенное понятие отношения: N-местное (N-арное) отношение R -Это множество упорядоченных наборов (Кортежей):
![]()
Множества Ai Не обязательно различны.
Свойства отношений
Пусть R Ì А2. Тогда отношение R Называется
Рефлексивным, Если " А ÎA ARa;
Антирефлексивным, Если " А ÎA ØАRа;
Симметричным, Если " А,B Î A ARb ![]() BRa;
BRa;
Антисимметричным, Если " А,B ÎA ARb& BRa ![]() A = B;
A = B;
Транзитивным, Если " А,B ÎA ARb & BRc ![]() ARc;
ARc;
Полным, Или Линейным, Если " А,B ÎA A ¹ B ![]() аRb Ú BRа.
аRb Ú BRа.
| < Предыдущая | Следующая > |
|---|