Глава 33. Теория алгоритмов. Основные сведения
Алгоритмом называется двусортное множество <Mp, R2>, где Mp – множество правил (процедур) решения задачи обладающих следующими свойствами:
1) детерминированности – однозначности применения этих правил на каждом шагу;
2) результативности – получения после применения этих правил информации, являющейся результатом;
3) массовости – инвариантности относительно входной информации;
4) элементарности (прозрачности) – отсутствия необходимости дальнейшего уточнения правил.
Алгоритмы, которые сводят решение поставленной задачи к арифметическим действиям над числами, называются Численными Алгоритмами.
Традиционным примером является известный алгоритм Евклида для нахождения наибольшего общего делителя двух заданных целых положительных чисел А и B. Алгоритм Евклида состоит из следующей системы последовательных указаний:
1) обозревай А и B и переходи к следующему;
2) сравни обозреваемые числа (А = B, или А < B, или А > b) и переходи к следующему;
3) если обозреваемые числа равны, то каждое из них дает искомый результат, если нет — переходи к следующему;
4) если первое обозреваемое число меньше второго, переставь их местами и переходи к следующему;
5) вычитай второе число из первого и обозревай два числа – вычитаемое и остаток;
6) переходи к указанию 2.
В математической форме данный алгоритм запишется следующим образом.
1) Пока A ¹ B выполнять шаг 2.
2) Замена текущей пары чисел (A, B) на пару – вычитаемое и остаток:
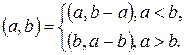
3) Получение значения наибольшего общего делителя:
C = a.
Численные алгоритмы получили широкое распространение благодаря тому, что к ним сводится решение многих задач (вычисление корней алгебраических уравнений, решение систем уравнений, численное дифференцирование и интегрирование и т. п.).
Существует другой тип алгоритмов, называемых Логическими, которые содержат предписания, относящиеся не к цифрам, а к объектам любой природы.
Типичным примером логических алгоритмов может служить алгоритм поиска пути в конечном лабиринте.
Лабиринт удобно изображать в виде графа, вершины которого соответствуют площадкам, а дуги — коридорам (рис.9.1).
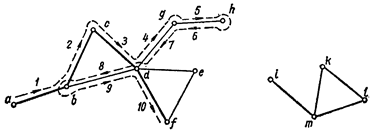
Рис. 9.1
Пусть требуется выяснить, достижима ли площадка из F площадки А, и если да, то найти путь из А в F, а если нет — вернуться в А. Лицо, ищущее путь в лабиринте, располагает нитью, конец которой закреплен на площадке А, и, двигаясь по лабиринту, может разматывать клубок (Р) или наоборот наматывать на него нить (Н). Можно делать отметки на проходимых коридорах и различать затем коридоры, еще ни разу не пройденные (зеленые — 3), пройденные один раз (желтые — Ж) и пройденные дважды (красные — К). Метод поиска может быть задан следующей схемой:
1) площадка F—остановка (цель достигнута);
2) петля — наматывание нити (от данной площадки расходятся, по крайней мере, два желтых коридора);
3) зеленая улица — разматывание нити (отданной площадки отходит хотя бы один зеленый коридор);
4) площадка А — остановка (исходный пункт);
5) отсутствие всех предыдущих признаков — наматывание нити.
Попав на какую-нибудь площадку, свериться со схемой признаков в указанном порядке и делать очередной ход в соответствии с первым же обнаруженным признаком, не проверяя остальных признаков. Такие ходы делаются до тех пор, пока не наступит остановка.
Богатый опыт разработки и применения алгоритмов подсказывает ряд общих свойств.
Дискретность алгоритма. Любой алгоритм можно рассматривать как процесс последовательного построения величин, идущий в дискретном времени по определенному предписанию, называемому Программой. В начальный момент задается конечная совокупность величин (исходные данные), а в каждый следующий момент совокупность величин получается по программе из совокупности, имевшейся в предыдущий момент.
Детерминированность алгоритма. Совокупность величин, получаемых в какой-то (не начальный) момент времени, однозначно определяется совокупностью величин, полученных в предшествующие моменты времени.
Алгоритм поиска пути в лабиринте допускает произвол в выборе коридора при наличии нескольких зеленых коридоров, отходящих от данной площадки. Чтобы сделать его строго детерминированным, необходимо добавить предписание о выборе зеленого коридора (например, первый по часовой стрелке).
Результативность (направленность) алгоритма. Если способ получения последующей величины из какой-нибудь заданной не приводит к результату, то должно быть указание, что надо считать результатом алгоритма. Иначе говоря, алгоритм через конечное число тактов времени (шагов) должен привести к остановке, которая свидетельствует о достижении требуемого результата.
В алгоритме поиска пути в лабиринте остановка наступает либо на достижимой площадке, либо при возвращении на исходную площадку, если указанная цель недостижима.
Массовость алгоритма. Алгоритм служит для решения целого класса задач, причем начальная совокупность величин может выбираться из некоторого множества.
В алгоритме Евклида числа А и B выбираются из бесконечного (счетного) множества целых чисел, а в алгоритме поиска пути в лабиринте начальная и конечная площадки выбираются из конечного множества площадок лабиринта. В математике проблема считается решенной, если для нее найден общий алгоритм.
Элементарность шагов алгоритма. Предписание о получении последующей совокупности величин из предшествующей должно быть простым и локальным. Это означает, что соответствующая операция должна быть элементарной для исполнителя алгоритма (человека или машины).
Встречающиеся в алгоритме Евклида операции сравнения, вычитания и перестановки чисел можно было бы расчленить на более простые операции, если бы они не считались достаточно стандартными и привычными. В то же время сам алгоритм Евклида может фигурировать в качестве элементарной операции более сложного алгоритма.
Алфавитом называется конечная система различных символов, называемых Буквами. Любая конечная последовательность П букв некоторого алфавита является Словом длины П в этом алфавите.
В алфавите из трех букв {А, B, С} словами будут последовательности B, ас, bac, Abbca, сbсссасаbса и т. д.
Если слово L является частью слова М, то говорят о вхождении слова L в слово М.
В слове Аbсbbсbаb имеются два вхождения слова Bсb и одно вхождение слова Bа.
В качестве операций ассоциативного исчисления определяется Система Допустимых Подстановок, с помощью которых одни слова преобразуются в другие. Подстановка вида L—М, где L и М — слова в том же алфавите, означает замену вхождения левой части правой, равно как и замену правой части левой. Иначе говоря, если в некотором слове R имеется одно или несколько вхождений слова L, то каждое из этих вхождений может заменяться словом М, и наоборот, если имеется вхождение слова М, то его можно заменить словом L.
Подстановка Ab—bсb применима четырьмя способами к слову Аbсbсbаb. Замена каждого из двух вхождений Bсb даст слова Ааbсbаb и Аbсаbаb, а замена каждого из двух вхождений Ab дает слова Bcbcbcbab, аbсbсbbсb. В то же время к слову Bасb Эта подстановка не применима. Подстановка вида Р—Æ означает, что из преобразуемого слова выбрасывается вхождение слова Р, а также что между двумя какими-либо буквами преобразуемого слова или впереди него, или за ним вставляется слово Р.
Таким образом, Ассоциативное Исчисление — это множество всех слов в некотором алфавите вместе с какой-нибудь конечной системой допустимых подстановок. Очевидно, чтобы задать ассоциативное исчисление, достаточно определить алфавит и систему допустимых подстановок
Алфавит {А, B, С, D, E} и система подстановок Ас—са, Ad—dA, Be—cb, Bd—db, Abac—abacc, Eca—ae, Edb—be).
Два слова называются Эквивалентными, если одно из них можно получить из другого последовательным применением допустимых подстановок.
Слова Abcde и Cadedb являются эквивалентными, что видно из следующих последовательных преобразований: Abcde, Acbde, Cabde, Cadbe, Cadedb.
Последовательность слов R1, R2, ..., Rn, когда каждое следующее слово является результатом однократного применения допустимой подстановки к предыдущему слову, образует Дедуктивную Цепочку, причем соседние слова в этой цепочке называют Смежными. Очевидно, любые два слова в дедуктивной цепочке являются эквивалентными.
Эквивалентность слов L и М обозначается L~М. Если L~М, то при наличии в каком-либо слове R вхождения L в результате подстановки L — М получается слово, эквивалентное R.
Воспользовавшись эквивалентностью Abcde~Cadbe, из слова Bbabcdec получаем эквивалентное ему слово Bbcadbec.
Рассмотрим конечное множество (Алфавит) М = {M1, M2, ..., Mn}, элементы которого будем называть Символами (буквами), а конечные последовательности символов — Словами.
Пусть Я0 — все множество слов, на длину которых не наложены никакие ограничения. Множество Я такое, что Я Ì Я0 называется Языком в алфавите М.
Пусть G — некоторая совокупность правил, с помощью которых в М порождаются все слова, принадлежащие языку Я, и только они. Совокупность правил G называется Грамматикой Языка Я.
Два языка называются Эквивалентными, если множества слов, из которых они состоят, совпадают. Две грамматики, G1 и G2, над Я называются Эквивалентными, если языки, ими порождаемые, эквивалентны.
Существует конечное множество состояний {S0, S1, ..., Sr} и каждому Sj (J = 1, 2, ..., R) сопоставляется набор пар вида (Mi, Sq), где I Î {1, 2, ..., R}, Q Î {0,1, ..., R}. Состоянию S0 сопоставляются пары вида (M0, Sh), где H Î {1, 2, ..., R). Символ M0 — специальный знак пробела между словами.
Конструирование слов происходит следующим образом: из состояния S0 переходим в любое состояние Sq. Из пар, сопоставленных выбранному состоянию Sq, берут любую пару (Mi, Sl). Этот выбор порождает следующее состояние Sl И первый символ слова Mi. Далее процесс построения слова происходит аналогично. Слово заканчивается при переходе к заключительному состоянию, как правило, S0.
Структуру языков удобно представлять в виде графа, вершины которого сопоставлены состояниям Sj, а дуги – парам (Mi, Sq) (рис.9.2).
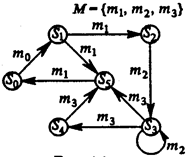
Рис. 9.2.
С помощью грамматики, задаваемой графом, порождается язык, который состоит из множества слов.
| < Предыдущая | Следующая > |
|---|