Глава 24. Графы. Определения графов
Основное определение
Графом G(V, E) называется совокупность двух множеств — непустого множества V (множества Вершин) и множества Е Неупорядоченных пар различных элементов множества V (Е — Множество Ребер).
G(V, E) = (V; E), V ¹ Æ, E Ì V´V, E = E-1.
Число вершин графа G Обозначим Р, А число ребер — Q:
P = P(G) = |V|, Q = Q(G) = |E|.
Смежность
Пусть V1, V2 — Вершины, Е = (V1, V2) — соединяющее их ребро. Тогда вершина V1 и ребро Е инцидентны, Вершина V2 и ребро Е Также инцидентны. Два ребра, инцидентные одной вершине, называются Смежными; Две вершины, инцидентные одному ребру, также называются Смежными.
Множество вершин, смежных с вершиной V, Называется Множеством смежности Вершины V И обозначается Г+(V):
Г+(v) = {u Î V | (u, v) Î E},
Г(V) = Г+(V) ![]() {V},
{V},
И Î Г(V) Û V Î Г(U).
Диаграммы
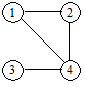
Обычно граф изображают Диаграммой: вершины — точками (или кружками), ребра — линиями (рисунок 6.1,А).
|
А) |
Б) |
Рис. 6.1. Диаграммы графов
Другие определения
Часто рассматриваются следующие родственные графам объекты.
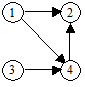
1. Если элементами множества Е Являются Упорядоченные Пары, то граф называется Ориентированным (или Орграфом). В этом случае элементы множества V называются Узлами, А элементы множества Е — дугами. (пример диаграммы орграфа приведен на рисунке 6.2,Б)
2. Если элементом множества Е Может быть пара Одинаковых (не различных) элементов V, То такой элемент множества Е Называется Петлей, А граф называется Графом с петлями (или Псевдографом).
3. Если Е Является не множеством, а Набором, Содержащим несколько одинаковых элементов, то эти элементы называются Кратными ребрами, А граф называется Мулътиграфом.
4. Если элементами множества Е Являются не обязательно двухэлементные, а Любые Подмножества множества V, То такие элементы множества Е Называются Гипердугами, А граф называется Гиперграфом.
5. Если задана функция F: V ® М И/или F: Е ® М, То множество М Называется множеством Пометок, А граф называется Помеченным (или Нагруженным). В качестве множества пометок обычно используются буквы или целые числа.
Изоморфизм графов
Говорят, что два графа G1(V1, E1) и G2(V2, E2) изоморфны (обозначается G1 ~ G2), если существует биекция H: V1 ® V2, Сохраняющая смежность:
E1 = (U, v) Î E1 Þ Е2 = (H(U), h(V)) ÎЕ2,
Е2 = (U, v) Î E2 Þ e1 = (H-1(U), h-1(V)) ÎE1.
Пример
Три внешне различные диаграммы, приведенные на рис. 6.2, являются диаграммами одного и того же графа К3, 3.
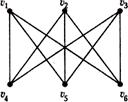
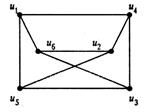
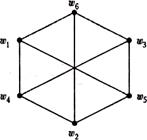
Рис. 6.2. Диаграммы изоморфных графов
| < Предыдущая | Следующая > |
|---|