Глава 23. Дифференцирование булевых функций
Производная первого порядка ![]() от булевой функции F по переменной XI Есть сумма по модулю 2 соответствующих остаточных функций:
от булевой функции F по переменной XI Есть сумма по модулю 2 соответствующих остаточных функций:
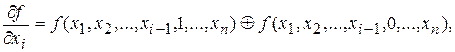
Где![]() – единичная остаточная функция;
– единичная остаточная функция;
![]() – нулевая остаточная функция
– нулевая остаточная функция
Производная первого порядка ![]() от булевой функции
от булевой функции ![]() Определяет условия, при которых эта функция изменяет значение при переключении переменной Xi (при переменной значения Xi на противоположное).
Определяет условия, при которых эта функция изменяет значение при переключении переменной Xi (при переменной значения Xi на противоположное).
Пример
Вычислим производную ![]() От булевой функции
От булевой функции![]() .
.
![]() . Согласно определению
. Согласно определению
![]() .
.
Смешанной производной ![]() От булевой функции F по переменным (
От булевой функции F по переменным (![]() называется выражение вида
называется выражение вида
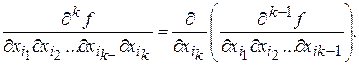
Смешанную производную K-го порядка ![]() вычисляют, определяя производную первого порядка K Раз фиксацией переменных
вычисляют, определяя производную первого порядка K Раз фиксацией переменных ![]() (порядок фиксации переменных не имеет значения); количество упорядочиваний равно K!
(порядок фиксации переменных не имеет значения); количество упорядочиваний равно K!
Производная K-го порядка ![]() От булевой функции
От булевой функции ![]() по переменным
по переменным ![]() Определяет условия, при которых эта функция изменяет значение при одновременном изменении значений переменных
Определяет условия, при которых эта функция изменяет значение при одновременном изменении значений переменных ![]() .
.
Упражнения
1. Проверить приведенные в теории равносильности путем построения таблиц истинности.
2. Построить СДНФ для Х1 | х2, х1 ¯ х2.
3. Минимизировать булеву функцию F(X1, X2, X3) = Ø(X1 Ú X1ØX2) ® ØX1X2X3, используя равносильности, операции склеивания и поглощения.
4. Минимизировать следующие функции с помощью диаграмм Вейча: F(X1, X2) = ØX1X2 ® X2, F(X1, X2, X3) = X1 ® ØX2 Ú ØX1ØX2(X3 Å ØX1), F(X1, X2, X3, X4) = ØX1X2 ® (X4 ¯ X3).
5. Проверить принадлежность классам Т0, Т1, T*, T<, ТL Функций ¯, |, Ú, ®, Å.
6. Определить ![]()
![]() для функции F(X1, X2, X3) = X1 ® ØX1ØX2(X3 Å ØX1).
для функции F(X1, X2, X3) = X1 ® ØX1ØX2(X3 Å ØX1).
| < Предыдущая | Следующая > |
|---|