8. Справочный материал

Правила дифференцирования.

Производная постоянной величины .

Производная суммы .

Производная разности .

Постоянный множитель можно выносить за знак производной:

.

Производная произведения

.

Производная частного

.

Производная сложной функции

.

Производная обратной функции

.

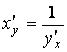Производная функции, заданной параметрически:

.

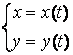
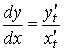Формула Лейбница для производной произведения функций

.

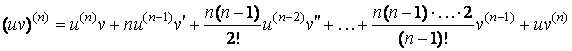Производные основных элементарных функций приведены в табл. 8.1.

Таблица 8.1 – Производные элементарных функций

В этой таблице – некоторый постоянный параметр. Структура таблицы позволяет установить аналогию и отличие между производными тригонометрических и гиперболических функций, а также производными обратных тригонометрических и обратных гиперболических функций. Здесь обозначены гиперболические и обратные гиперболические функции:

, , , ,

, ,

, .

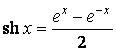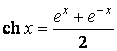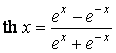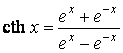Правила интегрирования.

Неопределенный интеграл

,

Где – первообразная подынтегральной функции , ; – произвольная постоянная.

Первообразные основных элементарных функций приведены в табл. 8.2.

Таблица 8.2 – Основные первообразные

В этой таблице – некоторый постоянный параметр.

Противоположность действий дифференцирования и интегрирования:

, .

Интеграл суммы

.

Постоянный множитель можно выносить за знак интеграла:

.

Интегрирование методом внесения под знак дифференциала: если

,

То при произвольной функции

.

Формула интегрирования по частям

.

Интегрирование методом замены переменных

,

Где – новая переменная, – обратная функция.

Теорема Барроу

.

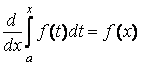Формула Ньютона-Лейбница

.

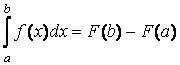< Предыдущая		Следующая >