6.3. Метод вариации произвольных постоянных
Рассмотрим общий метод интегрирования неоднородного линейного дифференциального уравнения вида (6.2), когда функция ![]() является произвольной непрерывной или кусочно-непрерывной функцией. Покажем, как найти решение неоднородного уравнения
является произвольной непрерывной или кусочно-непрерывной функцией. Покажем, как найти решение неоднородного уравнения ![]() , если известно решение соответствующего однородного уравнения
, если известно решение соответствующего однородного уравнения ![]() .
.
Пусть ![]() ,
, ![]() , …,
, …, ![]() – фундаментальная система решений однородного уравнения
– фундаментальная система решений однородного уравнения ![]() . Тогда его общее решение
. Тогда его общее решение
![]() , (6.5)
, (6.5)
Где ![]() ,
, ![]() , …,
, …, ![]() – произвольные постоянные.
– произвольные постоянные.
Будем искать общее решение неоднородного уравнения ![]() в таком же виде, а именно положим
в таком же виде, а именно положим
![]() , (6.6)
, (6.6)
Где ![]() ,
, ![]() , …,
, …, ![]() уже не произвольные постоянные, как в (6.5), а неизвестные пока что функции. Подставляя выражение (6.6) в неоднородное уравнение
уже не произвольные постоянные, как в (6.5), а неизвестные пока что функции. Подставляя выражение (6.6) в неоднородное уравнение ![]() и требуя, чтобы при этом выполнялось тождество, получим для нахождения
и требуя, чтобы при этом выполнялось тождество, получим для нахождения ![]() ,
, ![]() , …,
, …, ![]() лишь одно уравнение. Поэтому для того, чтобы эти
лишь одно уравнение. Поэтому для того, чтобы эти ![]() функций можно было найти однозначно, следует наложить на них
функций можно было найти однозначно, следует наложить на них ![]() каких-нибудь дополнительных условий. Покажем, как это сделать самым удобным способом.
каких-нибудь дополнительных условий. Покажем, как это сделать самым удобным способом.
Дифференцируя равенство (6.6), имеем
![]() .
.
Потребуем теперь, чтобы не только ![]() имело такой же вид, как
имело такой же вид, как ![]() , но чтобы и
, но чтобы и ![]() выглядело так же, как и
выглядело так же, как и ![]() , то есть, чтобы было
, то есть, чтобы было
![]() . (6.7)
. (6.7)
Для этого нужно потребовать выполнение равенства
![]() .
.
Это и есть первое из ![]() дополнительных условий.
дополнительных условий.
Дифференцируя равенство (6.7), получим
![]() .
.
Потребуем, чтобы ![]() выглядело так же, как и
выглядело так же, как и ![]() , то есть, чтобы было
, то есть, чтобы было
![]() .
.
Для этого нужно положить
![]() .
.
Это и есть второе дополнительное условие.
Аналогично, требуя, чтобы ![]() имело тот же вид, что и
имело тот же вид, что и ![]() , получим третье условие
, получим третье условие
![]() .
.
Продолжая этот процесс, на ![]() шаге потребуем, чтобы было
шаге потребуем, чтобы было
![]() . (6.8)
. (6.8)
Тогда придем к последнему из дополнительных условий
![]() .
.
Дифференцируя (6.8), имеем
![]()
![]() .
.
Итак, если выполняется система равенств
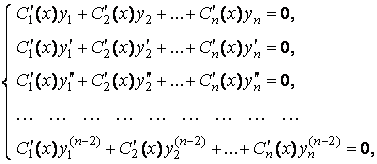 (6.9)
(6.9)
То
 (6.10)
(6.10)
Умножая равенства (6.10) соответственно на ![]() ,
, ![]() ,
, ![]() , …,
, …, ![]() , 1 и подставляя их в уравнение
, 1 и подставляя их в уравнение ![]() , получим
, получим
![]()
![]() .
.
Поскольку ![]() ,
, ![]() , …,
, …, ![]() есть решения уравнения
есть решения уравнения ![]() , то
, то
![]() ,
, ![]() , …,
, …, ![]() ,
,
А, значит,
![]() .
.
Это и есть то основное условие, по отношению к которому условия (6.9) являются дополнительными.
Таким образом, если для ![]() ,
, ![]() , …,
, …, ![]() выполнены условия
выполнены условия
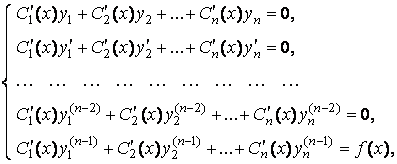 (6.11)
(6.11)
То функция (6.6) является решением уравнения ![]() .
.
Определителем неоднородной системы уравнений (6.11) является вронскиан ![]() , а так как функции
, а так как функции ![]() ,
, ![]() , …,
, …, ![]() линейно независимы, то
линейно независимы, то ![]() . Поэтому система (6.11) имеет единственное решение:
. Поэтому система (6.11) имеет единственное решение:
![]() ,
, ![]() , …,
, …, ![]() ,
,
Где ![]() ,
, ![]() , …,
, …, ![]() – некоторые функции, являющиеся кусочно-непрерывными, а, значит, и интегрируемыми. Поэтому получим
– некоторые функции, являющиеся кусочно-непрерывными, а, значит, и интегрируемыми. Поэтому получим
![]() ,
, ![]() , …,
, …, ![]() ,
,
Где ![]() ,
, ![]() , …,
, …, ![]() – независимые произвольные постоянные. Подставляя эти функции в равенство (6.6), находим
– независимые произвольные постоянные. Подставляя эти функции в равенство (6.6), находим
![]() . (6.12)
. (6.12)
Покажем, что это решение уравнения ![]() является его общим решением. Для этого перепишем равенство (6.12)
является его общим решением. Для этого перепишем равенство (6.12)
![]() . (6.13)
. (6.13)
Первая группа слагаемых справа есть общее решение однородного уравнения ![]() . Вторая же группа получается из функции (6.12), если положить в ней
. Вторая же группа получается из функции (6.12), если положить в ней ![]() . Но функция (6.12) удовлетворяет уравнению
. Но функция (6.12) удовлетворяет уравнению ![]() при любых
при любых ![]() ,
, ![]() , …,
, …, ![]() , поэтому вторая группа слагаемых соответствует частному решению
, поэтому вторая группа слагаемых соответствует частному решению ![]() этого уравнения. Следовательно, равенство (6.13) можно переписать в виде
этого уравнения. Следовательно, равенство (6.13) можно переписать в виде
![]() .
.
Отсюда и следует, что функция (6.13), или, что то же самое, функция (6.12) есть общее решение неоднородного линейного дифференциального уравнения (6.1).
Рассмотренный метод является обобщением метода, изложенного ранее для линейного дифференциального уравнения первого порядка, поэтому его также называют Методом вариации произвольных постоянных.
Пример 6.1. Найти общее решение уравнения
![]() .
.
Решение. Характеристическое уравнение ![]() имеет корни
имеет корни ![]() . Поэтому фундаментальная система решений соответствующего однородного уравнения состоит из функций:
. Поэтому фундаментальная система решений соответствующего однородного уравнения состоит из функций:
![]() ,
, ![]() .
.
Запишем общее решение однородного уравнения
![]() .
.
Тогда общее решение исходного неоднородного уравнения ищем как
![]() .
.
При ![]() система (6.11) примет вид:
система (6.11) примет вид:
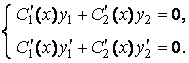
Для данного уравнения получим:
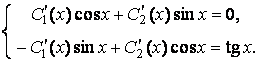
Эта система имеет решение:
 ,
, ![]() .
.
Интегрируя эти равенства, получим:
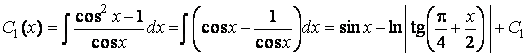 ,
,
![]() .
.
Запишем общее решение
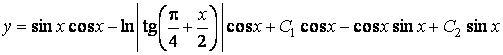 .
.
Окончательно
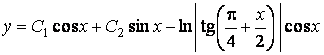 .
.
| < Предыдущая | Следующая > |
|---|