4.4. Понижение порядка однородного линейного уравнения
Практическое нахождение фундаментальной системы решений однородного линейного дифференциального уравнения (4.2), а значит и общего решения, иногда облегчает следующая теорема.
Теорема. Если известно одно частное решение Однородного линейного дифференциального уравнения (4.2), то порядок этого уравнения может быть понижен на единицу.
Доказательство. Пусть ![]() – решение дифференциального уравнения (4.2). Положим
– решение дифференциального уравнения (4.2). Положим ![]() , где
, где ![]() – новая неизвестная функция. Тогда формула (3.8) для линейного дифференциального оператора произведения двух функций дает
– новая неизвестная функция. Тогда формула (3.8) для линейного дифференциального оператора произведения двух функций дает
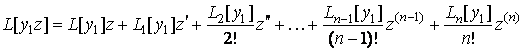 .
.
Поскольку ![]() , то
, то
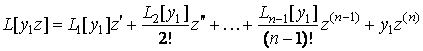 .
.
Поэтому однородное линейное дифференциальное уравнение (4.2) запишется так:
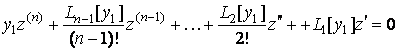 .
.
Полагая ![]() , получим
, получим
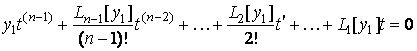 .
.
Таким образом, получено дифференциальное уравнение порядка ![]() .
.
Использование этой теоремы наиболее наглядно для уравнений второго порядка.
Рассмотрим уравнение второго порядка
![]() . (4.4)
. (4.4)
Пусть ![]() – известное частное решение этого уравнения. Положим
– известное частное решение этого уравнения. Положим ![]() . Тогда
. Тогда
![]() ,
, ![]() .
.
Подстановка в уравнение (4.4) дает
![]() ,
,
То есть
![]() .
.
А так как
![]() ,
,
То
![]() . (4.5)
. (4.5)
Полагая ![]() , приходим к уравнению
, приходим к уравнению
![]() . (4.6)
. (4.6)
Решая это уравнение, имеем:
![]() ,
,
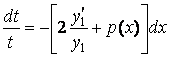 .
.
Отсюда
![]() ,
,
То есть
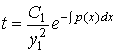 .
.
Это общее решение уравнения (4.6). Следовательно, общее решение уравнения (4.5) имеет вид
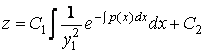 .
.
Можно положить ![]() ,
, ![]() . Тогда получим решение
. Тогда получим решение
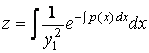 .
.
Таким образом, функция
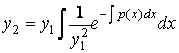 (4.7)
(4.7)
Является одним из решений уравнения (4.4).
Предположим, что решения ![]() и
и ![]() линейно зависимы. Тогда
линейно зависимы. Тогда
![]() ,
,
Откуда
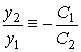 .
.
Между тем из (4.7) следует, что
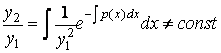 .
.
Поэтому ![]() и
и ![]() линейно независимы, а, значит, общее решение уравнения (4.4) дается формулой
линейно независимы, а, значит, общее решение уравнения (4.4) дается формулой
![]() ,
,
Где ![]() и
и ![]() – произвольные постоянные.
– произвольные постоянные.
Пример 4.1. Возьмем уравнение
![]() .
.
Легко видеть, что ![]() является решением этого уравнения. Приведем уравнение к виду (4.4)
является решением этого уравнения. Приведем уравнение к виду (4.4)
![]() .
.
Второе частное решение найдем по формуле (4.7):
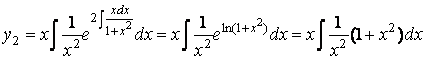 ,
,
 .
.
Итак, общее решение исходного дифференциального уравнения
![]() .
.
Примечание. Понизить порядок однородного линейного дифференциального уравнения (4.2) можно и на основании формулы Остроградского-Лиувилля
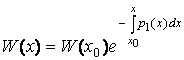 ,
,
Где ![]() – определитель Вронского для фундаментальной системы решений уравнения (4.2),
– определитель Вронского для фундаментальной системы решений уравнения (4.2), ![]() – некоторое значение переменной
– некоторое значение переменной ![]() .
.
| < Предыдущая | Следующая > |
|---|