12. Сводная таблица видов частных решений для различных видов правых частей

Таблица 1.

N	Правая часть дифф. уравнения	Корни Характеристиче­ского уравнения	Виды частного Решения
I.		1. Число не явля­ется корнем ха­рактеристиче­ского уравнения
2. Число – корень характеристиче­ского уравнения кратности
II.		1. Число не яв­ляется корнем характеристиче­ского уравнения
2. Число явля­ется корнем ха­рактеристиче­ского уравнения кратности
III.		1. Числа не являются кор­нями характери­стического урав­нения кратности
2. Числа яв­ляются корнями характеристиче­ского уравнения кратности
IV.		1. Числа не являются кор­нями характери­стического урав­нения кратности
2. Числа являются кор­нями характери­стического урав­нения кратности

Пример. Найти общее решение уравнения

.

Решение. Общее решение данного уравнения складывается из общего решения соответствующего ему однородного уравнения и частного решения данного уравнения, т. е. .

Найдем общее решение соответствующего однородного уравнения

.

Составим характеристическое уравнение и найдем его корни.

Поэтому общее решение однородного уравнения будет

2.Найдем частное решение данного уравнения. Так как в правой части его дан квадратный многочлен , и ноль не является корнем характеристиче­ского уравнения, то частное решение надо искать в виде (см. табл.1, случай I)

Где - неизвестные коэффициенты, которые нужно определить.

Так как выражение для является решением данного уравнения, то функ­ция и ее производные будучи подставлены в это уравнение удовле­творяют тождеству, т. е. сохраняют знак равенства в данном уравнении.

Найдем производные

Подставим эти выражения в данное уравнение и сгруппируем члены равенства по степеням :

.

Так как многочлены равны, то, следовательно, равны соответственные коэффи­циенты при одинаковых степенях , поэтому

Следовательно, частное решение будет иметь вид , а общее реше­ние данного уравнения будет

Пример. Найти общее решение уравнения .

Решение. Общее решение данного уравнения есть сумма общего решения соот­ветствующего однородного уравнения и частного решения :

1. Определим . Запишем соответственное уравнение . Через характеристическое уравнение находим его общее решение.

Поэтому

2.Определим частное решение .

Представим правую часть данного уравнения в виде (*):

Где - одночлен нулевой степени (вещественное число), а - одночлен первой степени (см. табл.1, случай III(1)). Так как не является корнем характеристичского уравнения, а То частное решение данного уравнения ищем в виде

Тогда

.

Так как является решением данного уравнения, то будучи подставленной в это уравнение вместе со своими производными она удовлетворяет равенству.

Подставим 1 в данное уравнение и сгруппируем по и , будем иметь

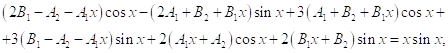
Или

Приравниваем коэффициенты в силу равенства выражений при и . Коэффициент при в правой части равен нулю, а при равен , по­этому будем иметь

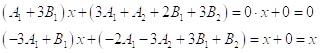
Так как многочлены равны, то, следовательно, равны их коэффициенты при одинаковых степенях . Приравнивая коэффициенты левых и правых частей равенств, получим систему относительно :

.

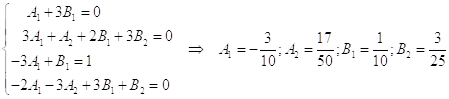Частное решение запишется

Общее решение данного уравнения

Рассмотрим случай, когда неоднородное уравнение имеет вид

. (6)

Для отыскания частного решения такого уравнения используется теорема:

Если - частное решение уравнения , а - частное решение уравнения , то есть частное решение уравнения (6).

Пример. Проинтегрировать уравнение

Решение. Общее решение данного уравнения

,

Где - общее решение соответственного данному однородного уравнения, - частное решение данного уравнения, где - частное решение урав­нения А - частное решение уравнения

1. Определим общее решение для уравнения

Общим решением уравнения будет

2. Определим частное решение уравнения .

Представим правую часть в виде (*)

.

Частное решение ищем в виде (см. табл.1, случай III (2)), так как число является корнем характеристического уравнения кратности :

,

Где и- некоторые вещественные числа и , которые нужно определить.

Итак, частное решение запишется выражением

Тогда

Из тождества которое получится после подстановки И в уравнение , определим и :

Приравниваем коэффициенты при И левой и правой части.

3. Определим частное решение Уравнения

В правой части имеем выражение вида , где . Частное реше­ние Уравнения ищем в виде (см. табл.1, случай II(1)):

,

вычислим производные

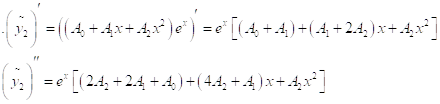
Из тождества, полученного после подстановки и В уравнение , определим коэффициенты :

Сократим на

.

Приравняем коэффициенты при одинаковых степенях левой и правой частей равенства.

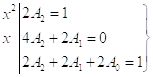, решая систему, получим .

Получили

Следовательно, общее решение данного уравнения

< Предыдущая		Следующая >