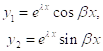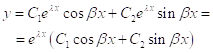11. Линейные дифференциальные уравнения второго порядка с постоян­ными коэффициентами

I. Рассмотрим однородные дифференциальные уравнения вида

(1)

Где - вещественные постоянные.

Для нахождения общего решения уравнения (1) поступаем так.

Составляем характеристическое уравнение для уравнения (1), в котором пока­затель степени соответствует порядку производной

А - корни уравнения (2).

Возможны следующие случаи:

A) - вещественные и различные

Тогда фундаментальная система частных решений уравнения (1) имеет вид:

,

Общим решением однородного уравнения будет

.

Б) Корни характеристического уравнения вещественные, но среди них есть кратные

Пусть, например, , т. е. - является -кратным корнем урав­нения (2), а все остальные корней различные.

В этом случае фундаментальная система частных решений имеет вид:

,

И общее решение будет

В) Среди корней характеристического уравнения есть комплексные

Пусть для определенностиА осталь­ные корни вещественные.

Фундаментальная система решений в этом случае будет иметь вид:

А общее решение записывается выражением

Пусть данное однородное уравнение второго порядка

(3)

Где - постоянные вещественные числа.

Если и - частные решения уравнения (3), то - есть общее решение этого уравнения. Для определения частных решений и уравнения (3) следует прежде решить характеристическое уравнение

. (4)

При решении квадратного уравнения (4) возможны три случая

Знак дис­кри­ми­нанта урав­нения (4)	Корни Уравнения (4)	Частные реше­ния уравнения (3)	Общее решение уравнения (3)
	Действитель­ные различ­ные
	Действитель­ные рав­ные
	Комплексные сопряженные

Пример. Найти общее решение дифференциального уравнения .

Решение. Составим характеристическое уравнение и решим его. Следовательно, корни действительные и различные, по­этому частными решениями будут, а общее решение .

Пример. Найти частное решение дифференциального уравнения , удовлетворяющее начальным условиям .

Решение. Составим характеристическое уравнение и решим его.

- корни действительные и равные. Частные решения в этом случае

Имеют вид ; общее решение будет

. (1)

Определим частное решение, удовлетворяющее начальным условиям:

. Но прежде вычислим производную :

(2)

В равенства (1) и (2) подставим начальные условия. Получим систему двух уравнений

.

Подставляя эти значения в общее решение, найдем частное:

.

Пример. Найти общее решение дифференциального уравнения

.

Решение. Составим и решим характеристическое уравнение .

Поэтому запишем его так: ,

Тогда

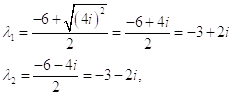
Т. е. мы имеем третий случай для которого

Частное решение имеет вид , общее решение

.

II. Рассмотрим теперь неоднородное уравнение

(5)

С постоянными вещественными коэффициентами . Отыскание об­щего решения неоднородного уравнения (5) сводится к отысканию общего ре­шения соответствующего однородного уравнения и к отысканию частного решения неоднородного уравнения (5)

,

где - общее решение однородного уравнения, а - частное решение неодно­родного уравнения.

В общем случае интегрирование уравнения (5) может быть осуществлено методом вариации произвольных постоянных. Для правых частей специального вида частное решение находится проще так называемым методом подбора, ко­торый возможно применить если вид правой части следующий:

(*)

Где и - многочлены степени и .

В этом случае частное решение неоднородного уравнения ищется в виде

Где а и - многочлены - ой степени общего вида с неопределенными коэффициентами, а - кратность корня характери­стического уравнения (если не является корнем характеристиче­ского уравнения, то ).

< Предыдущая		Следующая >