10. Некоторые виды дифференциальных уравнений высших порядков

I. Уравнения, содержащие только производную N-го порядка искомой функции и независимую переменную

или .

Этот вид уравнения допускает понижение порядка n-кратным интегрирова­нием, в результате этого получаем общее решение дифференциального уравнения.

Пример. Для данного дифференциального уравнения

Найти частное решение, удовлетворяющее начальным условиям:

Решение. Воспользуемся последовательным интегрированием.

.

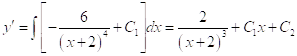
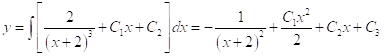Подставив последовательно в полученные равенства начальные условия, оп­ределим :

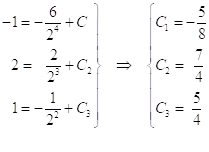
Частным решением данного уравнения будет

.

II. Уравнение не содержит искомой функции и ее производных до по­рядка (K-1) включительно:

. (1)

Порядок такого уравнения можно понизить на единиц заменой: , тогда уравнение (1) примет вид:

. (2)

Из уравнения (2), если это возможно, определяем , а за­тем находим Из уравнения

- кратным интегрированием.

В частном случае, когда , дифференциальное уравнение второго по­рядка , не содержит неизвестной функции , подстановкой приво­дится к уравнению первого порядка .

Пример. Проинтегрировать дифференциальное уравнение второго порядка

. (1)

Решение. Это уравнение не содержит . Положим в уравнении , тогда , получим линейное дифференциальное уравнение первого порядка отно­сительно неизвестной функции :

.

Воспользуемся подстановкой , тогда , получим

. (2)

Определяем , для этого положим . Получили уравнение с разде­ляющимися переменными.

Разделяем переменные и интегрируем

(полагаем ), тогда .

Определяем , для этого значение Подставим в уравнение (2):

или

,

Откуда , и т. к. , то следовательно, .

Возвращаясь к первоначальной переменной , получим

или

.

Это и будет общим решением данного уравнения.

Пример. Решить уравнение .

Решение. Уравнение не содержит искомую функцию и ее производные до третьего порядка включительно. Поэтому, полагая , получим . Подставим в данное уравнение значения и получим уравнение относи­тельно функции :

или .

Разделяем переменные и интегрируем

Тогда .

Последовательно интегрируя, найдем

,

.

Это выражение для и будет общим решением данного уравнения.

III. Уравнение не содержит независимого переменного X:

(1)

Подстановка позволяет понизить порядок уравнения на единицу. При этом рассматривается как новая неизвестная функция от : . Все про­изводные выражаются через производные от новой неизвест­ной функции . Для этой функции имеем

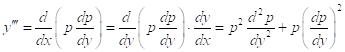И т. д.

Подставив эти выражения вместо в уравнение (1), получим диффе­ренциальное уравнение порядка.

Пример. Решить дифференциальное уравнение .

Решение. Так как данное уравнение не содержит независимой переменной , то полагая в этом уравнении , а , получим уравнение первого по­рядка:

.

Разделяя переменные и интегрируя, получим следующее

Так как , то .

Получим снова уравнение первого порядка, где неизвестной функцией является . Разделяя переменные и интегрируя, получим

.

Полученное выражение для есть решение данного уравнения.

Пример. Решить дифференциальное уравнение

.

Решение. Так как данное уравнение не содержит независимой переменной, то полагаем . Подставляя выражения для и в данное уравне­ние, получим дифференциальное уравнение первого порядка с разде­ляющимися переменными

.

Разделяя переменные и интегрируя, получим

1

.

Так как или .

Разделяя переменные и интегрируя, получим

.

Решением уравнения является .

< Предыдущая		Следующая >