09. Дифференциальные уравнения высших порядков

1. Общие понятия

Дифференциальным уравнением -го порядка называется уравнение вида

, (1)

Где - аргумент, - неизвестная функция.

Иногда рассматривается уравнение, разрешенное относительно старшей произ­водной

. (2)

Задача Коши дифференциального уравнения -го порядка состоит в том, чтобы найти решение данного уравнения, которое при заданном значении аргумента Принимает заданные значения , т. е. удовлетворяет началь­ным условиям

.

Геометрически задача Коши формируется следующим образом: среди всех интегральных кривых данного дифференциального уравнения выделить ту, которая проходит через наперед заданную точку и для которой при Имеют место равенства

.

Решение задачи Коши называют частным решением уравнения (1).

Функция , где - произвольные постоянные, называ­ется общим решением уравнения (1) в некоторой области на плоскости xOy, если при соответствующем выборе значений эта функция обраща­ется в любое частное решение, график которого лежит в области .

При дифференциальные уравнения (1) и (2) будут уравнениями вто­рого порядка:

.

Их общее решение зависит от двух произвольных постоян­ных .

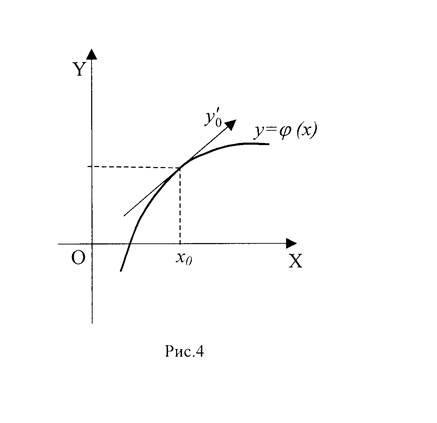
Общее решение можно рассмат­ривать как семейство интегральных кривых данного дифференциального уравнения, зависящее от параметров и . Частному решению, получен­ному из общего, соответствует одна кривая этого семейства. Задача Коши для дифференциального уравнения второго порядка состоит в том, чтобы найти интегральную кривую, проходящую через данную точку в задан­ном направлении (см. рис.4).

< Предыдущая		Следующая >