08. Уравнение Бернулли

Уравнение Бернулли имеет вид

где

( при и это уравнение является линейным ). С помо­щью замены пере­менной уравнение Бернулли приводится к линейному уравнению и интегрируется как линейное.

Пример 1. Решить уравнение Бернулли

или .

Решение. Умножим обе части на :

. (1)

Положим замену т. к. то есть вычислим . Тогда

или (2)

Подставим (2) в уравнение (1), получим линейное уравнение:

или

Разделим переменные

.

Проинтегрируем обе части

.

Отсюда получаем общее решение исходного уравнения

Замечание. Уравнение Бернулли может быть проинтегрировано также методом вариаций постоянной, как и линейное уравнение, и с помощью подстановки .

Пример. Решить уравнение Бернулли

. (1)

Решение. Применим метод вариации произвольной постоянной.

1. Найдем общее решение соответствующего однородного уравнения

или . (2)

2. Разделяя переменные и интегрируя получим общее решение уравнения (2)

- общее решение (2).

3. Общее решение данного уравнения (1) ищем в виде (где - но­вая неизвестная функция). Следовательно при подстановке функции и ее производной в уравнение (1) должно сохраняться тожде­ство

Подставим выражения для и В (1):

,

преобразуя полученное выражение, получим

или .

4. Для нахождения получим уравнение с разделяющимися перемен­ными, из которого, разделяя переменные и интегрируя, найдем

.

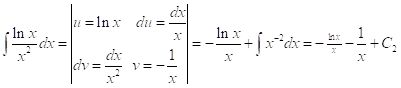Таким образом имеем:

.

Подставим полученное значение в выражение общего решения дан­ного уравнения, найдем решение уравнения (1)

.

Уравнение называется уравнением в полных диф­ференциалах, если его левая часть является полным дифференциалом некоторой функции :

.

Для этого необходимо и достаточно, чтобы

.

В этом случае есть общий интеграл данного уравнения. Функция может быть найдена из системы уравнений:

.

Рассмотрим на примерах, как интегрируются уравнения в полных диффе­ренциалах.

Пример. Найти общий интеграл дифференциального уравнения

.

Решение. Проверим, что данное уравнение является уравнением в полных дифференциалах. В данном случае и так как

и , то левая часть уравнения есть полный дифференциал некоторой функции , для которой

.

По данной частной производной найдем значение с точно­стью до произвольной функции :

( Можно было бы начинать с равенства И находить с точно­стью до произвольной функции ).

Продифференцируем найденную функцию по :

.

Приравнивая уже известному нам значению

(см. выше), получим

, откуда .

Определив функцию , можем записать

И, следовательно, общим интегралом уравнения будет , что рав­носильно (где ).

< Предыдущая		Следующая >