13. Системы дифференциальных уравнений
Мы ограничимся здесь рассмотрением систем дифференциальных уравнений первого порядка с двумя и тремя неизвестными функциями. Переход к общему случаю не представляет каких-либо принципиальных затруднений.
Определение 1. Нормальная система двух дифференциальных уравнений называется линейной системой первого порядка, если она имеет вид
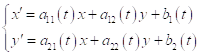 (1)
(1)
Определение 2. Линейная система дифференциальных уравнений (1) называется однородной, если ![]()
В дальнейшем обратимся лишь к частному случаю – однородной линейной системе с постоянными коэффициентами.
Решением системы (1) называется всякий набор из двух функций
![]() , (2)
, (2)
Обращающих оба уравнения системы (1) в тождество.
Задача Коши для системы (1) состоит в том, чтобы найти такое решение (2), которое при ![]() принимало бы заданные значения (начальные условия)
принимало бы заданные значения (начальные условия)
![]()
Общее решение системы содержит две произвольные постоянные ![]() и
и ![]() , фиксируя которые, находят любое частное решение.
, фиксируя которые, находят любое частное решение.
Геометрически решение (2) определяет некоторую линию ( интегральную кривую системы) на плоскости ![]() . Если считать, что аргумент
. Если считать, что аргумент ![]() играет роль времени, то указанная кривая будет служить траекторией точки, движущейся на плоскости
играет роль времени, то указанная кривая будет служить траекторией точки, движущейся на плоскости ![]() .
.
Тат как в этом случае ![]() определяет вектор скорости, то с механической точки зрения система (1) означает задание поля скоростей в каждый момент времени
определяет вектор скорости, то с механической точки зрения система (1) означает задание поля скоростей в каждый момент времени ![]() , а решение задачи Коши равносильно нахождению траектории точки, движущейся под воздействием этого поля и занимавшей в начальный момент времени
, а решение задачи Коши равносильно нахождению траектории точки, движущейся под воздействием этого поля и занимавшей в начальный момент времени ![]() положение
положение ![]() . Плоскость
. Плоскость ![]() , на которой рассматривается движение называется Фазовой.
, на которой рассматривается движение называется Фазовой.
Нормальная система трех уравнений первого порядка имеет вид:
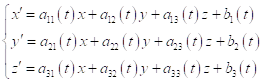
![]() (3)
(3)
Все основные понятия и определения, сказанные выше для системы двух уравнений, повторяются и для системы (3) с той лишь разницей, что добавляется везде третья функция ![]() , а вместо фазовой плоскости надо рассматривать фазовое пространство
, а вместо фазовой плоскости надо рассматривать фазовое пространство ![]() .
.
Для решения системы дифференциальных уравнений может быть использован обычный метод исключения неизвестных, сводящий систему (1) к одному дифференциальному уравнению от неизвестной функции второго порядка, а систему (3) – к дифференциальному уравнению третьего порядка. Если метод исключения применяется к линейной системе, то получается также линейное дифференциальное уравнение, к решению которого можно применять выше рассмотренные методы.
Пример. Решить задачу Коши для линейной системы

Решение. Запишем систему в виде

И, применяя метод исключения, выразим из первого уравнения ![]() через
через ![]() и
и ![]() :
:
![]() После подстановки
После подстановки ![]() во второе уравнение будем иметь ( при
во второе уравнение будем иметь ( при ![]() ):
):
![]()
Получили неоднородное дифференциальное уравнение с постоянными коэффициентами второго порядка. Используя метод решения такого вида уравнений, рассмотренный выше, получим его общее решение
![]()
А так как ![]() было выражено через
было выражено через ![]() , то вычисляя производную
, то вычисляя производную ![]() и подставив
и подставив ![]() выражение
выражение
![]()
Получим общее решение данной системы
![]()
![]() .
.
Теперь обратимся к начальным условиям, используя которые, определим постоянные ![]() и
и ![]() .
.
Так как ![]() , то при
, то при ![]() имеем
имеем
![]()
И так как ![]() ,
, ![]() , следовательно,
, следовательно,
![]()
Получим систему

Таким образом, решением данной задачи Коши являются функции
![]()
Пример. Проинтегрировать систему уравнений
![]()
Или 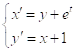
Решение. Из первого уравнения данной системы находим ![]() и подставим его производную
и подставим его производную ![]() во второе уравнение системы, тогда получим
во второе уравнение системы, тогда получим ![]() .
.
Уравнение ![]() второго порядка неоднородное с постоянными коэффициентами. Для решения этого уравнения воспользуемся методом решения для этого вида уравнения, рассмотренным выше.
второго порядка неоднородное с постоянными коэффициентами. Для решения этого уравнения воспользуемся методом решения для этого вида уравнения, рассмотренным выше.
Общее решение уравнения ![]() будет функция
будет функция ![]() .
.
Так как ![]() , то, вычислив производную
, то, вычислив производную![]() , подставим ее выражение в это равенство
, подставим ее выражение в это равенство
![]() .
.
Общее решение системы
![]()
![]() .
.
Пример. Найти общее решение системы
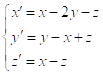 ,
,
Где ![]() - неизвестные функции.
- неизвестные функции.
Решение. Исключим ![]() из этих уравнений; для этого из третьего уравнения найдем
из этих уравнений; для этого из третьего уравнения найдем ![]() .
.
Продифференцируем полученное равенство по ![]() :
: ![]() , подставив значения
, подставив значения ![]() и
и ![]() в первое уравнение, найдем из него
в первое уравнение, найдем из него ![]() , следовательно,
, следовательно, ![]() .
.
Подставив значения ![]() во второе уравнение системы, будем иметь
во второе уравнение системы, будем иметь
![]() или
или ![]() .
.
Получили линейное однородное дифференциальное уравнение третьего порядка. Составим характеристическое уравнение и найдем его корни

Следовательно, ![]() - общее решение уравнения будет
- общее решение уравнения будет
![]() .
.
Чтобы определить неизвестные функции ![]() и
и ![]() , найдем
, найдем ![]() и
и ![]() из последнего равенства:
из последнего равенства:
![]() ,
,
Откуда
![]()
![]() .
.
Общим решением данной системы будет система функций
![]()
![]()
![]() .
.
Для интегрирования однородных линейных систем с постоянными коэффициентами применяется также Метод Эйлера.
Пусть дана однородная линейная система дифференциальных уравнений
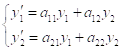 (4)
(4)
Где ![]() .
.
Определение. Линейной комбинацией вектор-функций ![]() и
и ![]() на интервале
на интервале ![]() называется вектор-функция
называется вектор-функция ![]() .
.
Теорема. Пусть вектор-функция

Решения на ![]() однородной системы (4). Тогда любая их комбинация
однородной системы (4). Тогда любая их комбинация ![]() также есть решение на
также есть решение на ![]() этой системы.
этой системы.
Рассмотрим на конкретном примере метод Эйлера.
Пример. Решить систему
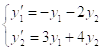 .
.
Решение. Искомыми функциями являются функции ![]() .
.
Составим характеристический многочлен для данной системы
![]() .
.
Находим корни характеристического уравнения
![]()
Составим для ![]() вспомогательную алгебрагическую систему
вспомогательную алгебрагическую систему
![]() :
: 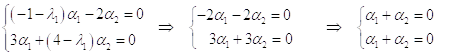
Получили систему, имеющую бесчисленное множество решений. Выразим ![]() через
через ![]() :
:![]() и пусть
и пусть ![]() , тогда
, тогда ![]() . Тогда вектор-функция
. Тогда вектор-функция ![]() - это первое фундаментальное решение.
- это первое фундаментальное решение.
Составим вспомогательную алгебрагическую систему для ![]()
![]() :
: 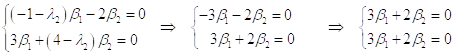
Получили систему с бесчисленным множеством решений; выразим ![]() через
через ![]() :
:
![]() и пусть
и пусть ![]() , тогда
, тогда ![]() .
.
Тогда вектор-функция ![]() - второе фундаментальное решение.
- второе фундаментальное решение.
Итак, фундаментальная система решений состоит из двух вектор-функций
![]()
![]() .
.
Следовательно, вся совокупность решений системы есть множество

| < Предыдущая |
|---|