1.1. Предмет теории дифференциальных уравнений

Часто законы, связывающие изучаемые величины, исследователю неизвестны, но он может установить зависимость между этими величинами и их производными. Например, в инженерной практике возникает задача определения закона движения тела под влиянием действующих на тело сил. Найти такой закон движения непосредственно было бы нелегко. В этом случае применяют основной закон динамики в виде второго закона Ньютона : «сила равна произведению массы на ускорение ». Этот закон в дифференциальной форме позволяет установить зависимость, содержащую ускорение как вторую производную пути по времени :

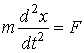. (1.1)

Закон движения будет найден, если научиться определять неизвестную функцию пути из дифференциального уравнения (1.1). Основная задача теории дифференциальных уравнений и заключается в изучении методов нахождения неизвестных функций, определяемых дифференциальными уравнениями. Предметом изучения в теории дифференциальных уравнений являются методы решения и исследования дифференциальных уравнений и их систем.

Вначале дифференциальные уравнения возникли при рассмотрении отдельных конкретных задач в работах Декарта, Галилея, Барроу (учитель Ньютона), Ферма, Кеплера в XVII веке. В то время понятие производной еще не было введено, как и сам термин «дифференциальное уравнение». История дифференциальных уравнений как самостоятельного раздела математики началась с работ Исаака Ньютона и Готфрида Вильгельма Лейбница, основателей дифференциального и интегрального исчисления. Сам термин «дифференциальное уравнение» введен Лейбницем. Он также ввел некоторые поныне используемые обозначения. Существенный вклад в теорию дифференциальных уравнений внесли братья Якоб и Иоганн Бернулли (ученики Лейбница), потомки Иоганна Бернулли (особенно Даниил), Леонард Эйлер (ученик Иоганна Бернулли), Лагранж, Лиувилль, Коши и другие известные математики.

К составлению и решению дифференциальных уравнений приводят многочисленные задачи как самой математики, так и других наук – физики, химии, техники, биологии, экономики. Математические модели многих реальных динамических объектов и систем управления представляют собой дифференциальные уравнения или их системы, поэтому теория дифференциальных уравнений является основой математического моделирования и теории автоматического управления.

Только простейшие дифференциальные уравнения допускают аналитическое решение. Для большинства дифференциальных уравнений, связанных с практическими задачами, необходимо использовать численные методы решения. Однако основным фундаментом численных методов решения дифференциальных уравнений остается классическая теория дифференциальных уравнений.

< Предыдущая		Следующая >