4.2.4. Примеры решения задач по теме «Экстремумы»

Задача 1.

Найти стационарную точку функции

Указание

В стационарной точке

Решение

Следовательно, координаты стационарной точки можно найти как решение системы

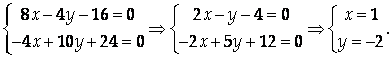
Ответ: (1,-2).

Задача 2.

Найти точку минимума функции

Указание

Пусть М0 – стационарная точка,

Тогда М0 является точкой минимума, если D > 0, A > 0.

Решение

Найдем стационарные точки функции:

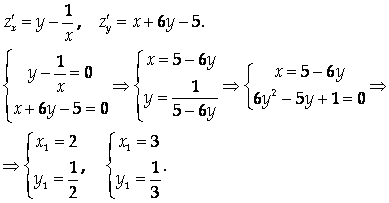
Итак, стационарные точки функции –

Исследуем их на экстремум.

Нет экстремума.

Ответ:

Задача 3.

Найти экстремум функции

При условии 2Х + 5У + 3 = 0.

Указание

Найдите экстремум функции Лагранжа

Решение

Исследуем на экстремум функцию Лагранжа

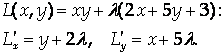
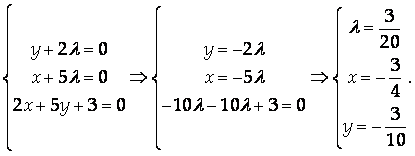
Исследуем найденную точку на экстремум:

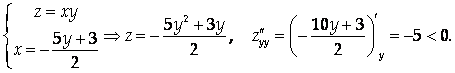
Следовательно, Точка условного максимума, и значение функции в этой точке равно

Ответ:

Задача 4.

На параболе

Найти точку, ближайшую к прямой Х – У = 2.

Указание

Расстояние от точки М(Х0, У0) до прямой Х – У = 2 определяется по формуле

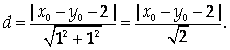
Следовательно, требуется найти минимум функции

При условии

Решение

Расстояние от точки М(Х0, У0) до прямой Х – У = 2 определяется по формуле

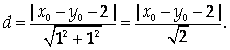
Следовательно, требуется найти минимум функции

При условии

Составим функцию Лагранжа:

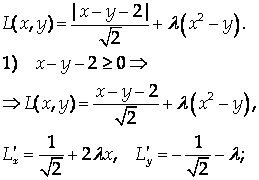
Не выполнено условие на знак подмодульного выражения.

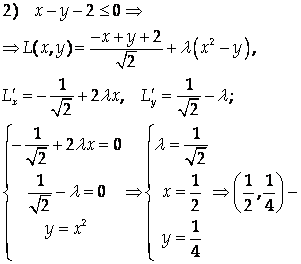
Стационарная точка. При этом

Следовательно, найдена точка условного минимума.

Ответ:

Задача 5.

Найти множество значений функции

Указание

Найдите наибольшее и наименьшее значение функции в данной области,

Которые могут достигаться либо на границе, либо в стационарной точке внутри области.

Решение

Найдем стационарные точки функции:

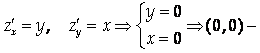
Стационарная точка, Z(0,0) = 0.

Для определения наибольшего и наименьшего значения функции на границе области найдем условный экстремум функции Z = Xy при условии X2 + Y2 = 1.

Составим функцию Лагранжа:

Итак, найдены четыре стационарные точки:

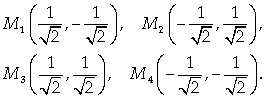
При этом

Следовательно, наименьшее и наибольшее значения достигаются на границе области, а так как функция непрерывна, она принимает внутри области все промежуточные значения между наименьшим и наибольшим, то есть множество ее значений в данной области –

Ответ:

< Предыдущая		Следующая >