5.1.1. Справочный материал

Основные элементарные функции

6. Степенная функция У = хα,

7. Показательная функция У = ах, A > 0, A1.

8. Логарифмическая функция Y=logAx, A > 0, A1.

9. Тригонометрические функции: Y = sin X, Y = cos X, Y = tg X, Y = ctg X, Y = sec X, Y = cosec X.

10. Обратные тригонометрические функции: Y = arcsin X, Y = arсcos X, Y = arctg X, Y = arcctg X, Y = arcsec X, Y = arccosec X.

Определение предела

Число А называется Пределом функции у = F(X) при х, стремящемся к х0, если

Такое, что

Обозначение:

1-й замечательный предел

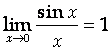
Cледствия из первого замечательного предела

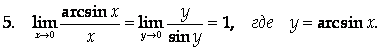
2-й замечательный предел

Следствия из второго замечательного предела

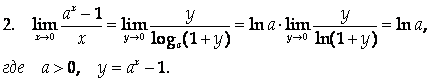
Гиперболические функции

Определение производной

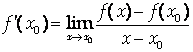
Уравнение касательной

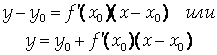
Правила дифференцирования

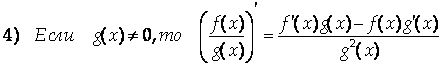
Таблица основных производных

№	F(x)	F΄(x)	№	F(x)	F΄(x)
1	C	0	9	Ctgx
2	Xα	αxα-1	10	Shx	Chx
3	Ax	Axlna	11	Chx	Shx
4	Ex	Ex	12	Thx
5	Lnx		13	Cthx
6	Sinx	Cosx	14	Arcsinx
7	Cosx	-sinx	15	Arccosx
8	Tgx		16	Arctgx
			17	Arcctgx

Логарифмическое дифференцирование

Правило Лопиталя

Формула Тейлора

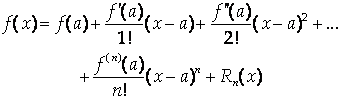
Частные производные

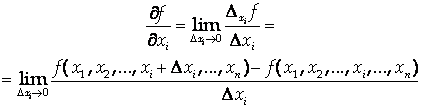
< Предыдущая		Следующая >