4.2.3. Нахождение наибольших и наименьших значений
Пусть функция U = F (X1 , X2 ,…, Xn) определена и непрерывна в некотором ограниченном и замкнутом множестве D и имеет на этом множестве конечные частные производные (за исключением, быть может, отдельных точек). Тогда эта функция достигает на D своего наибольшего и наименьшего значения (см. свойства непрерывных функций). Если это значение достигается во внутренней точке множества, то, очевидно, эта точка должна быть стационарной; кроме того, наибольшее и наименьшее значение может достигаться на границе множества D. Поэтому для определения наибольшего и наименьшего значений функции на множестве D требуется:
1) найти стационарные точки функции, принадлежащие D, и вычислить значения функции в этих точках;
2) найти наибольшее и наименьшее значение, принимаемое функцией на границе множества D;
3) выбрать наименьшее и наибольшее из полученных чисел, которые и будут являться наименьшим и наибольшим значениями функции на всем множестве D.
Примеры.
1. Найдем наибольшее значение функции Z = Sin X + sin Y – sin (X + Y) в треугольнике со сторонами Х = 0, у = 0, Х + у = 2π. Стационарные точки определяются из решения системы
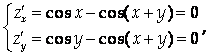
Откуда
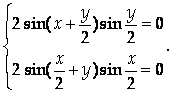
Единственной внутренней точкой данного треугольника, являющейся решением полученной системы, будет
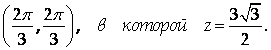
Это значение оказывается наибольшим и на всем рассматриваемом множестве, так как на его границе Z = 0.
2. Найдем наибольшее и наименьшее значения функции Z = X² + Y² - 12X + 16Y в области X² + Y² ≤ 25.
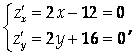
Откуда Х =6, У = -8 – точка, не лежащая в заданном круге. Следовательно, наибольшее и наименьшее значения данная функция принимает на границе области, то есть на окружности X² + Y² = 25. Составим функцию Лагранжа
L (X, Y ) = X² + Y² - 12X + 16Y + L(X² + Y² - 25).
Ее стационарные точки найдем из системы
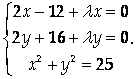
![]()
Получим
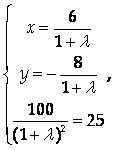
Откуда L1 =1, L2 = -3. Следовательно, стационарными точками являются
(3, -4) и (-3, 4). В первой из них Z = -75, во второй Z = 125. Эти числа являются наименьшим и наибольшим значениями Z в заданной области.
| < Предыдущая | Следующая > |
|---|