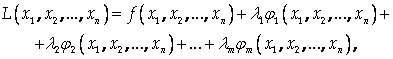4.2.2. Условный экстремум

Если аргументы функции F (X1 , X2 ,…, Xn) связаны дополнительными условиями в виде M Уравнений (M < N):

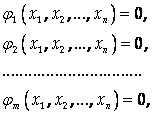
Где функции JI имеют непрерывные частные производные, то эти уравнения называются Уравнениями связи.

Экстремум функции F (X1 , X2 ,…, Xn) При выполнении уравнений связи называется Условным экстремумом.

Замечание. Можно предложить следующее геометрическое истолкование условного экстремума функции двух переменных: пусть аргументы функции F(X,Y) связаны уравнением J(х, у) = 0, задающим некоторую кривую в плоскости ОХу. Восставив из каждой точки этой кривой перпендикуляры к плоскости ОХу до пересечения с поверхностью Z = F (X,Y), получим пространственную кривую, лежащую на поверхности над кривой J(х, у) = 0. Задача состоит в поиске точек экстремума полученной кривой, которые, разумеется, в общем случае не совпадают с точками безусловного экстремума функции F(X,Y).

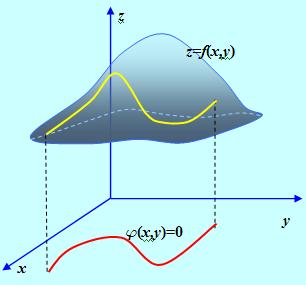
Рис. 1

Определим необходимые условия условного экстремума для функции двух переменных, введя предварительно следующее определение:

Функция Где LI – Некоторые постоянные, называется Функцией Лагранжа, а числа LI – Неопределенными множителями Лагранжа.

Теорема 3 (необходимые условия условного экстремума). Условный экстремум функции Z = F (X, Y) при наличии уравнения связи J(Х, у) = 0 может достигаться только в стационарных точках функции Лагранжа

Доказательство.

Уравнение связи задает неявную зависимость У от Х, поэтому будем считать, что У есть функция от Х: У = у(х). Тогда Z есть сложная функция от Х, и ее критические точки определяются условием:

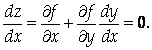
Из уравнения связи следует, что

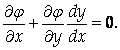
Умножим последнее равенство на некоторое число λ и сложим с предыдущим равенством. Получим:

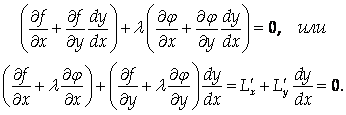
Последнее равенство должно выполняться в стационарных точках, откуда следует:

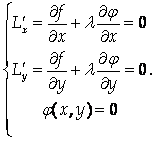
Получена система трех уравнений относительно трех неизвестных: Х, у и L, причем первые два уравнения являются условиями стационарной точки функции Лагранжа. Исключая из системы (5.6) вспомогательное неизвестное L, находим координаты точек, в которых исходная функция может иметь условный экстремум.

Замечание 1. Проверку наличия условного экстремума в найденной точке можно провести с помощью исследования частных производных второго порядка функции Лагранжа по аналогии с теоремой 2.

Замечание 2. Точки, в которых может достигаться условный экстремум функции F (X1 , X2 ,…, Xn) При выполнении уравнений связи, можно определить как решения системы

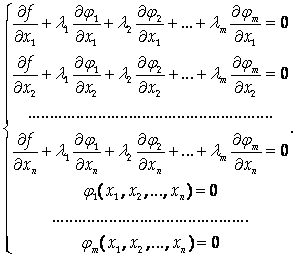
Пример. Найдем условный экстремум функции Z = Xy при условии Х + у = 1. Составим функцию Лагранжа L(X, Y) = Xy + L(X + Y – 1). Система для определения стационарных точек при этом выглядит так:

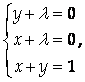
Откуда -2L=1, L=-0,5, Х = у = -L = 0,5. При этом L (X, Y) можно представить в виде

L (X, Y) = -0,5 (X – Y)² + 0,5 ≤ 0,5,

Поэтому в найденной стационарной точке L (X, Y)Имеет максимум, а Z = Xy – Условный максимум.

< Предыдущая		Следующая >