4.2.1. Экстремумы
|
Точка М0 (х0 , у0 ) называется Точкой максимума функции Z = F (X, Y), если F (Xo , YO) > F (X, Y) Для всех точек (х, у) из некоторой окрестности точки М0. |
|
Точка М0 (х0 , у0 ) называется Точкой минимума функции Z = F (X, Y), если F (Xo , YO) < F (X, Y) Для всех точек (х, у) из некоторой окрестности точки М0. |
Замечание 1. Точки максимума и минимума называются Точками экстремума Функции нескольких переменных.
Замечание 2. Аналогичным образом определяется точка экстремума для функции от любого количества переменных.
Теорема 1 (необходимые условия экстремума). Если М0 (х0 , у0 ) – точка экстремума функции Z = F (X, Y), то в этой точке частные производные первого порядка данной функции равны нулю или не существуют.
Доказательство.
Зафиксируем значение переменной У, считая У = у0. Тогда функция F (X, Y0) будет функцией одной переменной Х, для которой Х = х0 является точкой экстремума. Следовательно, по теореме Ферма
![]()
Или не существует. Аналогично доказывается такое же утверждение для
![]()
Точки, принадлежащие области определения функции нескольких переменных, в которых частные производные функции равны нулю или не существуют, называются Стационарными точками этой функции.
Замечание. Таким образом, экстремум может достигаться только в стационарных точках, но не обязательно он наблюдается в каждой из них.
Примеры.
1. Найдем стационарную точку функции Z = X² + Y². Для этого решим систему уравнений
![]()
Откуда Х0 = у0 = 0. Очевидно, что в этой точке функция имеет минимум, так как при Х = у = 0 Z = 0, а при остальных значениях аргументов Z > 0.
2. Для функции Z = Xy стационарной точкой тоже является (0, 0), но экстремум в этой точке не достигается ( Z (0, 0) = 0, а в окрестности стационарной точки функция принимает как положительные, так и отрицательные значения).
Теорема 2 (достаточные условия экстремума). Пусть в некоторой окрестности точки М0 (х0 , у0 ) , являющейся стационарной точкой функции Z = F (X, Y), эта функция имеет непрерывные частные производные до 3-го порядка включительно. Обозначим
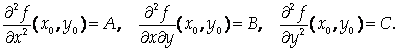
Тогда:
1) F (X, Y) имеет в точке М0 максимум, если AC – B² > 0, A < 0;
2) F (X, Y) имеет в точке М0 минимум, если AC – B² > 0, A > 0;
3) экстремум в стационарной точке отсутствует, если AC – B² < 0;
4) если AC – B² = 0, необходимо дополнительное исследование.
Доказательство.
Напишем формулу Тейлора второго порядка для функции F (X, Y), помня о том, что в стационарной точке частные производные первого порядка равны нулю:

Если угол между отрезком М0М , где М (х0+DХ, у0+DУ), и осью ОХ обозначить J, то DХ = DR cosJ, DY = DRSinJ. При этом формула Тейлора примет вид:
![]()
Пусть ![]() Тогда можно разделить и умножить выражение в скобках на А. Получим:
Тогда можно разделить и умножить выражение в скобках на А. Получим:
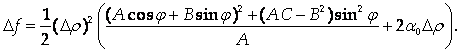
Рассмотрим теперь четыре возможных случая:
1) AC-B² > 0, A < 0. Тогда

При достаточно малых DR. Следовательно, в некоторой окрестности М0 F (X0 + DX, Y0 + DY) < F (X0 , Y0), то есть М0 – точка максимума.
2) Пусть AC – B² > 0, A > 0. Тогда
![]()
И М0 – точка минимума.
3) Пусть AC-B² < 0, A > 0. Рассмотрим приращение аргументов вдоль луча J = 0. Тогда из ранее доказанного следует, что
![]()
То есть при движении вдоль этого луча функция возрастает. Если же перемещаться вдоль луча J = J0 такого, что tg J0 = -A/B, То
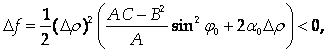
Следовательно, при движении вдоль этого луча функция убывает. Значит, точка М0 не является точкой экстремума.
3`) При AC – B² < 0, A < 0 доказательство отсутствия экстремума проводится аналогично предыдущему.
3``) Если AC – B² < 0, A = 0, то ![]() При этом
При этом
![]()
Тогда при достаточно малых J выражение 2B cosJ + C sinJ близко к 2В, то есть сохраняет постоянный знак, а sinJ меняет знак в окрестности точки М0 . Значит, приращение функции меняет знак в окрестности стационарной точки, которая поэтому не является точкой экстремума.
4) Если AC – B² = 0, а ![]() ,
, ![]() , то есть знак приращения определяется знаком 2A0. При этом для выяснения вопроса о существовании экстремума необходимо дальнейшее исследование.
, то есть знак приращения определяется знаком 2A0. При этом для выяснения вопроса о существовании экстремума необходимо дальнейшее исследование.
Пример. Найдем точки экстремума функции Z = X² - 2Xy + 2Y² + 2X. Для поиска стационарных точек решим систему
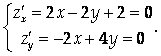
Итак, стационарная точка (-2,-1). При этом А = 2, В = -2, С = 4. Тогда AC – B² = 4 > 0, следовательно, в стационарной точке достигается экстремум, а именно минимум (так как A > 0).
| < Предыдущая | Следующая > |
|---|