4.1.4. Примеры решения задач по теме «Производная по направлению. Градиент»

Задача 1.

Составить уравнение касательной плоскости к поверхности

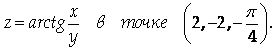
Указание

Уравнение касательной плоскости к поверхности

В точке (Х0, Y0, Z0) имеет вид:

Решение

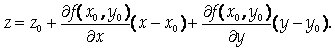
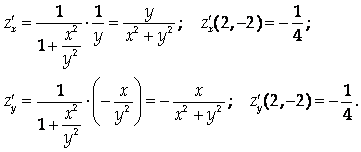
Подставим эти значения в уравнение касательной плоскости:

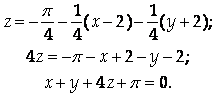
Ответ:

Задача 2.

Составить уравнение касательной плоскости к поверхности

В точке (1,2,-1).

Указание

Найдите частные производные Z по Х и У как производные неявной функции:

Решение

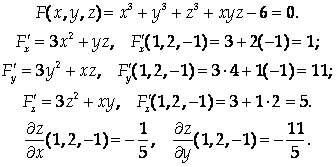
Уравнение касательной плоскости:

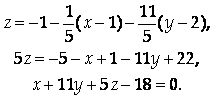
Ответ:

Задача 3.

Составить уравнения нормали к поверхности

В точке (0,4,2).

Указание

Будем называть нормалью прямую, проходящую через данную точку перпендикулярно касательной плоскости, проведенной через эту точку. Тогда канонические уравнения нормали выглядят так:

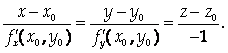
Решение

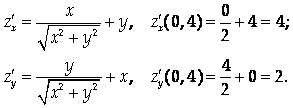
Следовательно, канонические уравнения нормали:

Ответ:

Задача 4.

Найти производную функции

И точке М(2,-4) по направлению вектора MN, если N(-1,-8).

Указание

Производная функции Z = F (X, Y) в точке (Х0, У0) по направлению L, заданному вектором А = (Ха, Уа, Za), имеет вид:

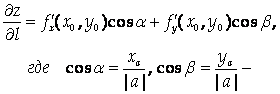
Направляющие косинусы направления L.

Решение

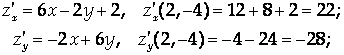
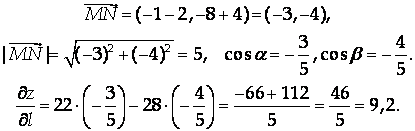
Ответ: 9,2.

Задача 5.

Найти производную функции

В точке (3,2,1) по направлению, образующему с координатными осями равные тупые углы.

Указание

Причем

Решение

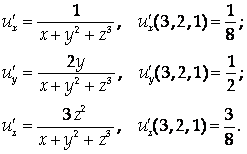
Найдем направляющие косинусы направления L, используя свойство направляющих косинусов:

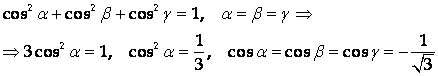
(поскольку косинус тупого угла отрицателен).

Тогда

Ответ:

Задача 6.

Найти градиент функции

В точке А(6,10,-5).

Указание

Воспользуйтесь формулой

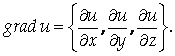
Решение

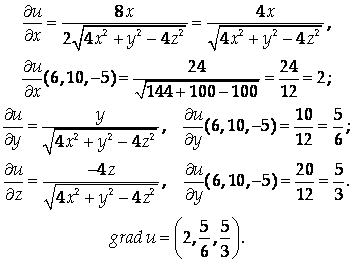
Ответ:

< Предыдущая		Следующая >