3.3.4. Примеры решения задач по теме «Неявные функции. Производные высших порядков»
Задача 1.
Найти ![]() в точке (1,0), если
в точке (1,0), если
![]()
Указание
Воспользуйтесь формулой
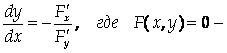
Уравнение, задающее неявную функцию.
![]()
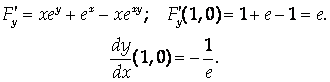
Ответ: ![]()
Задача 2.
Функция Z = Z(X,Y) задана неявно:
![]()
Найти ![]()
Указание
Если Х, У – независимые переменные, а функция Z = Z(X,Y) задана неявно:
![]()
То
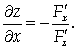
Найдем полную производную функции F по переменной Х, считая У независимой переменной, Z – неизвестной функцией от Х, и учитывая то, что функция F тождественно равна нулю, следовательно, и любая ее производная тоже равна нулю.
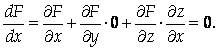
Отсюда

Ответ: 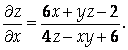
Задача 3.
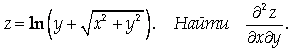
Указание
Воспользуйтесь формулой
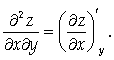
Решение

Упростим полученное выражение:

Теперь найдем частную производную этой функции по У:

Ответ: 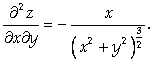
Задача 4.
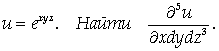
Указание
Продифференцируйте функцию по Х, затем полученное выражение – по У, а затем результат – три раза по Z.
Решение
![]()

Ответ: ![]()
Задача 5.
Найти значение параметра А, при котором функция
![]()
Удовлетворяет уравнению
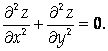
Указание
Найдите соответствующие производные 2-го порядка, а затем определите значения А, при которых указанное равенство выполняется в какой-либо конкретной точке (например, при Х = у = 0).
Решение


Поскольку условие
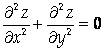
Должно выполняться при любых значениях Х и У, положим Х = у = 0. Тогда
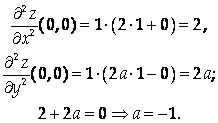
Следовательно, либо указанное равенство выполняется для Всех значений Х, У при А = -1, либо задача не имеет решений. Найдем значение выражения
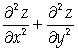
При А = -1:

Итак, при А = -1 функция
![]()
Удовлетворяет уравнению
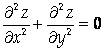
При всех Х, У.
Ответ: А = -1.
Задача 6.
Найти дифференциал 2-го порядка от функции
![]()
Указание
Воспользуйтесь формулой
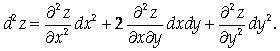
Решение
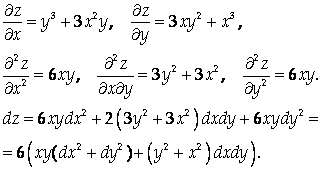
Ответ: ![]()
| < Предыдущая | Следующая > |
|---|