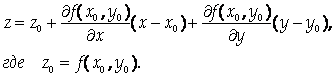4.1.1. Геометрические приложения производной
Пусть функция Z = F (X, Y) является дифференцируемой в окрестности точки М (х0 , у0). Тогда ее частные производные
![]()
Являются угловыми коэффициентами касательных к линиям пересечения поверхности Z = F (X, Y) С плоскостями У = у0 И Х = х0, которые будут касательными и к самой поверхности Z = F (X, Y). Составим уравнение плоскости, проходящей через эти прямые. Направляющие векторы касательных имеют вид
![]()
Поэтому нормаль к плоскости можно представить в виде их векторного произведения:
![]()
Следовательно, уравнение плоскости можно записать так:
|
Плоскость, определяемая этим уравнением, называется Касательной плоскостью к графику функции Z = F (X, Y) в точке с координатами (х0 ,у0 ,Z0 ). |
Из определения дифференцируемой функции следует, что приращение функции F в окрестности точки М можно представить в виде:
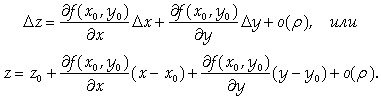
Следовательно, разность между аппликатами графика функции и касательной плоскости является бесконечно малой более высокого порядка, чем R, При ![]()
При этом дифференциал функции F имеет вид:
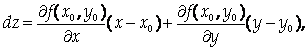
Что соответствует Приращению аппликаты касательной плоскости к графику функции. В этом состоит геометрический смысл дифференциала.
|
Ненулевой вектор, перпендикулярный касательной плоскости в точке М (х0 , у0) поверхности Z = F (X, Y), называется Нормалью к поверхности в этой точке. |
В качестве нормали к рассматриваемой поверхности удобно принять вектор
![]()
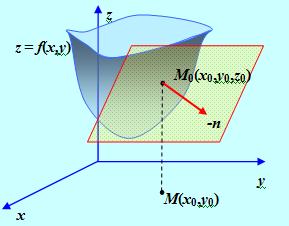
Рис. 1
Пример.
Составим уравнение касательной плоскости к поверхности Z = Xy в точке М (1; 1). При Х0 = у0 = 1 Z0 =1;
![]()
Следовательно, касательная плоскость задается уравнением: Z = 1 + (X – 1) + (Y – 1), или X + Y – Z – 1 = 0. При этом вектор нормали в данной точке поверхности имеет вид: N = {1; 1; -1}.
Найдем приращение аппликат графика функции и касательной плоскости при переходе от точки М К точке N(1,01; 1,01).
ΔZ = 1,01² - 1 = 0,0201; ΔZКас = (1,01 + 1,01 – 1) – (1 + 1 – 1) = 0,02. Следовательно,
Dz = ΔZКас = 0,02. При этом ΔZ – Dz = 0,0001.
| < Предыдущая | Следующая > |
|---|