3.3.3. Дифференциалы высших порядков

Дифференциалом второго порядка функции U = F (X, Y, Z) называется

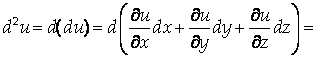
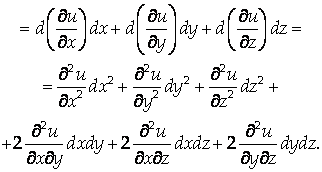
Аналогично можно определить дифференциалы 3-го и более высоких порядков:

Дифференциалом порядка K называется полный дифференциал от дифференциала порядка (K – 1): D K U = D (D K-1 U).

Свойства дифференциалов высших порядков

1. K-й дифференциал является однородным целым многочленом степени K относительно дифференциалов независимых переменных, коэффициентами при которых служат частные производные K-го порядка, умноженные на целочисленные постоянные (такие же, как при обычном возведении в степень):

2. Дифференциалы порядка выше первого не инвариантны относительно выбора переменных.

< Предыдущая		Следующая >