3.2.3. Дифференцирование сложных функций
Пусть аргументы функции Z = F (X, Y) являются, в свою очередь, функциями переменных U и V: X = X (U, V), Y = Y (U, V). Тогда функция F тоже есть функция от U и V. Выясним, как найти ее частные производные по аргументам U и V, Не делая непосредственной подстановки
Z = F ( X(U, V), Y(U, V)). При этом будем предполагать, что все рассматриваемые функции имеют частные производные по всем своим аргументам.
Зададим аргументу U приращение DU, не изменяя аргумент V. Тогда
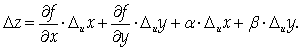
Если же задать приращение только аргументу V, получим:
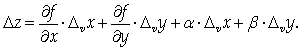
Разделим обе части первого равенства на DU, а второго – на DV и перейдем к пределу соответственно при
![]()
Учтем при этом, что в силу непрерывности функций х И У
![]()
Следовательно,
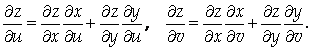
Рассмотрим некоторые частные случаи.
Пусть X = X(T), Y = Y(T). Тогда функция F (X,Y) является фактически функцией одной переменной T , и можно, используя полученные формулы и заменяя в них частные производные Х и У по U И V на обычные производные по T (разумеется, при условии дифференцируемости функций X(T) И Y(T) ) , получить выражение для ![]()
![]()
Предположим теперь, что в качестве T выступает переменная Х, то есть Х и У связаны соотношением У = у (х). При этом, как и в предыдущем случае, функция F является функцией одной переменной Х. Используя предыдущую формулу при T = X и учитывая, что
![]()
Получим, что
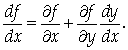
Обратим внимание на то, что в этой формуле присутствуют две производные функции F по аргументу Х: слева стоит так называемая Полная производная, в отличие от частной, стоящей справа.
Примеры.
1. Пусть Z = Xy, Где X = U² + V, Y = Uv². Найдем ![]() и
и ![]() . Для этого предварительно вычислим частные производные трех заданных функций по каждому из своих аргументов:
. Для этого предварительно вычислим частные производные трех заданных функций по каждому из своих аргументов:

Тогда
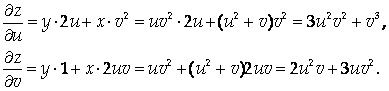
(В окончательный результат подставляем выражения для Х И У как функций U и V).
2. Найдем полную производную функции Z = Sin (X + Y²), где Y = Cos X.
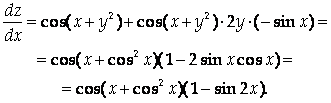
| < Предыдущая | Следующая > |
|---|