3.2.1. Дифференциал. Производные сложных функций

При исследовании вопросов, связанных с дифференцируемостью, ограничимся случаем функции трех переменных, поскольку все доказательства для большего количества переменных проводятся так же.

Полным приращением функции U = F(X, Y, Z) называется

Теорема 1. Если частные производные

Существуют в точке (Х0 , у0 , Z0) и в некоторой ее окрестности и непрерывны в точке (X0 , Y0 , Z0) , то

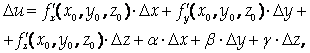
Где α, β, γ – бесконечно малые, зависящие от DХ, DУ, DZ.

Доказательство.

Представим полное приращение ΔU в виде:

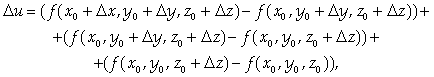
Где каждая разность представляет собой частное приращение функции только по одной из переменных. Из условия теоремы следует, что к этим разностям можно применить теорему Лагранжа. При этом получим:

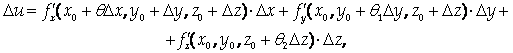
Так как по условию теоремы частные производные непрерывны в точке (Х0 , у0 , Z0), можно представить их в виде:

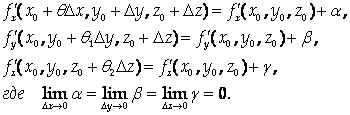
Теорема доказана.

Можно показать, что

Где

Действительно, α, β и γ – бесконечно малые при а

Ограниченные (т. к. их модули не превышают 1).

Тогда приращение функции, удовлетворяющей условиям теоремы 1, можно представить в виде:

Если приращение функции U = F (X, Y, Z) в точке (X0 , Y0 , Z0) можно представить в виде

то функция называется Дифференцируемой в этой точке, а выражение

Главной линейной частью приращения или полным дифференциалом рассматриваемой функции.

Обозначения: Du, Df (X0 , Y0 , Z0).

Так же, как в случае функции одной переменной, дифференциалами независимых переменных считаются их произвольные приращения, поэтому

Замечание 1. Итак, утверждение «функция дифференцируема» не равнозначно утверждению «функция имеет частные производные» - для дифференцируемости требуется еще и непрерывность этих производных в рассматриваемой точке.

Замечание 2. Если в последней формуле считать

Частными дифференциалами данной функции (как функции одного из аргументов), то можно сказать, что полный дифференциал равен сумме частных дифференциалов:

< Предыдущая		Следующая >