3.1.8. Примеры решения задач по теме «Предел и непрерывность. Частные производные»

Задача 1.

Определить вид линий уровня функции

Указание

Уравнения линий уровня:

Решение

Определим вид линий, задаваемых уравнениями

Ответ: гиперболы.

Задача 2.

Дана область:

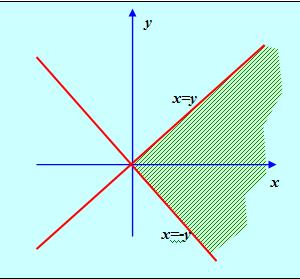
Рис. 3

И функции:

1) 2) 3)

4) 5)

Для какой из них данная область является областью определения?

Указание

Найдите область определения каждой из данных функций, учитывая соответствующие ограничения (подкоренные выражения должны быть неотрицательными, логарифмируемые выражения – положительными, знаменатели дробей – не равными нулю, а аргумент арксинуса может принимать значения только из отрезка [0,1]).

Решение

Найдем область определения каждой из данных функций:

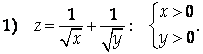
Эта система неравенств задает первую четверть координатной плоскости:

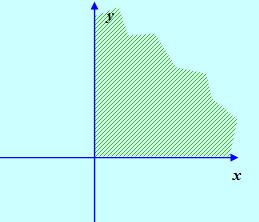
Рис. 4

То есть не совпадает с приведенным рисунком.

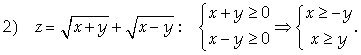
Именно эта область приведена на рисунке.

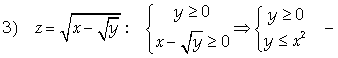
Область, ограниченная снизу осью Ох, а сверху – параболой У = х2:

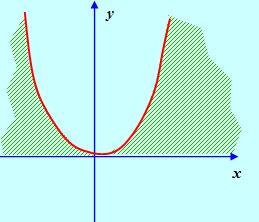
Рис. 5

Точки, лежащие в первой и третьей координатных четвертях:

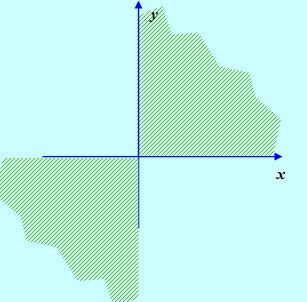
Рис. 6

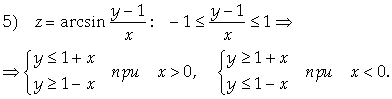
Соответствующая область выглядит так:

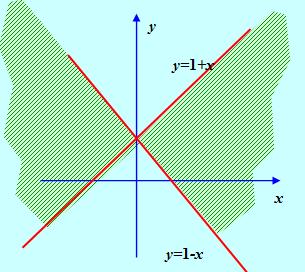
Рис. 7

Ответ: приведена область определения функции

Задача 3.

Найти повторные пределы

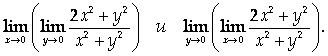
Указание

При вычислении предела по одному из аргументов остальные аргументы выступают как параметры.

Решение

Ответ: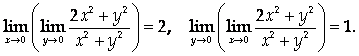

Задача 4.

Найти частные производные функции

В точке (1,1).

Указание

При дифференцировании функции нескольких переменных по одному из

аргументов остальные аргументы выступают как параметры.

Решение

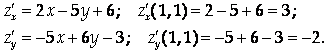
Ответ:

Задача 5.

Найти частную производную по У функции

Указание

Поскольку и основание степени, и показатель зависят от У, нужно применить формулу логарифмического дифференцирования.

Решение

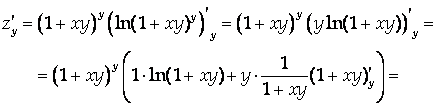
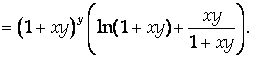
Ответ: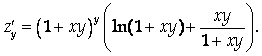

Задача 6.

Для функции

Найти

Указание

При дифференцировании функции нескольких переменных по одному из аргументов остальные аргументы выступают как параметры.

Решение

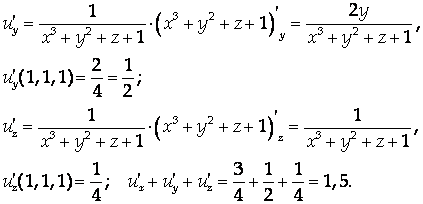
Ответ: 1,5.

< Предыдущая		Следующая >