3.1.7. Функции двух переменных

Рассмотрим уравнение поверхности Z = F (X,Y) и проведем плоскость Х = const. Выберем на линии пересечения плоскости с поверхностью точку М (х, у).

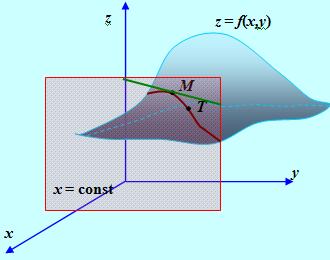
Рис. 2

Если задать аргументу У приращение ΔУ и рассмотреть точку Т на кривой с координатами (Х, у+ΔУ, Z+ΔyZ), то тангенс угла, образованного секущей МТ с положительным направлением оси ОУ, будет равен . Переходя к пределу при , получим, что частная производная равна тангенсу угла, образованного касательной к полученной кривой в точке М с положительным направлением оси ОУ. Соответственно частная производная равна тангенсу угла с осью ОХ касательной к кривой, полученной в результате сечения поверхности Z = F (X,Y) плоскостью Y = Const.

< Предыдущая		Следующая >