3.1.6. Частные производные
Рассмотрим изменение функции
![]()
При задании приращения только одному из ее аргументов – ХI , и назовем его ![]()
|
Частной производной функции
По аргументу ХI называется
|
Обозначения:
![]()
Таким образом, частная производная функции нескольких переменных определяется фактически как производная функции Одной переменной – хI. Поэтому для нее справедливы все свойства производных, доказанные для функции одной переменной.
Замечание. При практическом вычислении частных производных пользуемся обычными правилами дифференцирования функции одной переменной, полагая аргумент, по которому ведется дифференцирование, переменным, а остальные аргументы – постоянными.
Примеры.
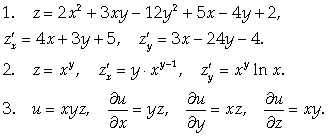
| < Предыдущая | Следующая > |
|---|
