2.7.1. Выпуклость. Асимптоты. Общая схема исследования функции

Кривая называется Выпуклой (обращенной выпуклостью вверх) на интервале (Ab), если все точки кривой лежат ниже любой ее касательной на этом интервале.

Кривая называется Вогнутой (обращенной выпуклостью вниз) на интервале (Ab), если все точки кривой лежат выше любой ее касательной на этом интервале.

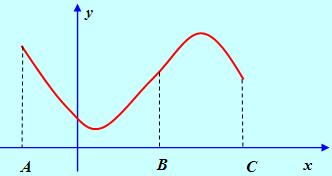
Рис. 1

Например, кривая, изображенная на рисунке, выпукла на интервале (ВС) и вогнута на интервале (АВ).

Теорема 1. Если F''(X) < 0 во всех точках интервала (Ab), то кривая Y = F(X) выпукла на этом интервале. Если F’’(X) > 0 во всех точках интервала (Ab), то кривая Y = F(X) вогнута на этом интервале.

Доказательство.

Докажем первое утверждение теоремы. Пусть F’’(X) < 0 на (Ab).

Выберем на интервале (Ab) произвольную точку Х = х0 и докажем, что все точки кривой на этом интервале лежат ниже проведенной в точке с

Абсциссой Х0 касательной, то есть ордината любой точки кривой на рассматриваемом интервале меньше ординаты касательной.

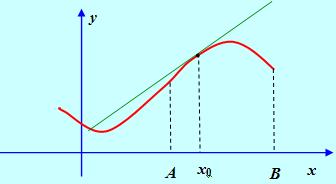
Рис. 2

Уравнение кривой имеет вид Y = F(X), а уравнение касательной при Х = х0:

Тогда

Применив теорему Лагранжа, получим:

где С лежит между Х и Х0. Применим к первому множителю правой части полученного равенства еще раз теорему Лагранжа:

(здесь С1 – между Х0 и С). Пусть X > X0.

Рис. 3

Тогда

Поэтому

Если же X < X0, то

Рис. 4

Но при этом по-прежнему

Таким образом, любая точка кривой на данном интервале лежит ниже касательной в точке с абсциссой Х0. Следовательно, кривая является выпуклой.

Второе утверждение теоремы доказывается аналогичным образом.

Точка, отделяющая выпуклую часть непрерывной кривой от вогнутой, называется Точкой перегиба.

Замечание. Если в точке перегиба существует касательная к кривой, то в этой точке она пересекает кривую, потому что по одну сторону от данной точки кривая проходит выше касательной, а по другую – ниже.

Теорема 2 (необходимое условие точки перегиба). Если в точке X0 Перегиба кривой, являющейся графиком функции Y = F(X), существует вторая производная F’’(X), то F’’(X0) = 0.

Доказательство.

Так как при х = х0

По формуле Тейлора получаем:

Если бы , разность сохраняла бы постоянный знак в некоторой окрестности точки Х0 , в то время как в точке перегиба эта разность должна менять знак. Следовательно, F’’(X0) = 0.

Теорема 3 ( достаточное условие точек перегиба). Если функция Y = F(X) дифференцируема в точке Х0 , дважды дифференцируема в проколотой окрестности этой точки и F’’(X) меняет знак при Х = х0 , то Х0 – точка перегиба.

Доказательство.

В теореме 1 показано, что знак разности определяется знаком F’’(C1), так как (C – X0)(X – X0) > 0 по обе стороны точки Х0. Следовательно, меняет знак при Х = х0, то есть Х0 – точка перегиба.

Замечание. Можно доказать, что если в условиях теоремы 5 из лекции 10 критическая точка не является точкой экстремума, то она является точкой перегиба.

Пример. Найдем интервалы выпуклости и вогнутости и точки перегиба функции

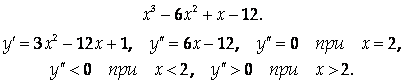
Таким образом, график функции является выпуклым при х < 2, вогнутым при Х > 2, а Х = 2 – точка его перегиба.

< Предыдущая		Следующая >