2.6.5. Примеры решения задач по теме «Монотонность и экстремумы»

Задача 1.

Найти интервалы возрастания функции

Указание

Найдите интервалы, принадлежащие области определения функции, на которых ее производная положительна.

Решение

Область определения функции:

Найдем производную и исследуем ее знак.

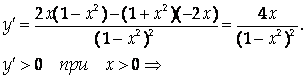
С учетом области определения интервалы возрастания:

Ответ:

Задача 2.

Найти точку максимума функции

Указание

Требуется найти критическую точку, в которой знак производной меняется с плюса на минус.

Решение

Область определения функции:

Найдем критические точки функции:

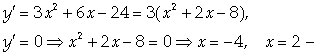
Критические точки.

Исследуем знак производной на интервалах, разделенных критическими точками:

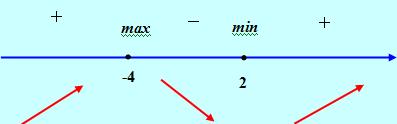
Рис. 3

Ответ: Х = -4.

Задача 3.

Найти точку минимума функции

Указание

Не забывайте, что критическими точками функции являются не только точки, в которых производная равна нулю, но и точки, в которых производная не существует (если сама функция определена в этой точке).

Решение

Область определения функции:

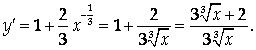
Функция имеет две критические точки:

Исследуем знак производной на интервалах, разделенных критическими точками:

Рис. 4

При этом график функции имеет вид:

Рис. 5

Ответ: Х = 0.

Задача 4.

Найти наименьшее значение функции

На отрезке [-5,12].

Указание

Функция, непрерывная на отрезке, принимает на нем наименьшее значение либо на границе, либо в критической точке, расположенной внутри отрезка.

Решение

Область определения функции:

То есть на отрезке [-5,12] функция определена и непрерывна.

Найдем критические точки:

Единственная критическая точка на отрезке [-5,12]: Х = 0.

Следовательно, наименьшее значение функции может достигаться в одной из трех точек: Х = -5, Х = 0 или Х = 12.

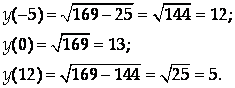
Итак, наименьшее значение функции

На отрезке [-5,12] равно 5.

Ответ: 5.

Задача 5.

Число 12 разложить на два положительных множителя так, чтобы сумма их квадратов была наименьшей.

Указание

Найдите минимум функции

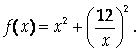
Решение

Пусть Х – один из множителей, тогда второй: и требуется найти точку минимума функции

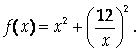
Область определения функции:

Следовательно, критические точки:

По условию множители должны быть положительными, поэтому исследуем знак производной только при X > 0:

Рис. 6

Итак,

Ответ:

< Предыдущая		Следующая >