2.4.2. Раскрытие неопределенностей
Если функции F(X) И G(X) удовлетворяют на некотором отрезке [Ab] условиям теоремы Коши и F(A) = G(A) = 0, то отношение F(X)/G(X) Не определено при Х=а, но определено при остальных значениях Х. Поэтому можно поставить задачу вычисления предела этого отношения при ![]() Вычисление таких пределов называют обычно «раскрытием неопределенностей вида {0/0}».
Вычисление таких пределов называют обычно «раскрытием неопределенностей вида {0/0}».
Теорема 3 (правило Лопиталя). Пусть функции F(X) и G(X) Удовлетворяют на отрезке [Ab] условиям теоремы Коши и F(A)=G(A)=0. Тогда, если существует
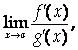
То существует и
![]()
Причем
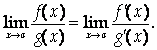
Доказательство.
Выберем
![]()
Из теоремы Коши следует, что
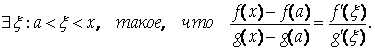
По условию теоремы F(A)=G(A)=0, поэтому
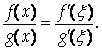
При ![]()
![]() . При этом, если существует
. При этом, если существует

То существует и
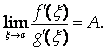
Поэтому
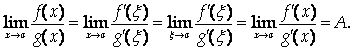
Теорема доказана.
Пример.
При A > 0
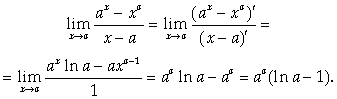
Замечание 1. Если F(X) Или G(X) Не определены при Х=а, можно доопределить их в этой точке значениями F(A)=G(A)=0. Тогда обе функции будут непрерывными в точке А, и к этому случаю можно применить теорему 3.
Замечание 2. Если F’(A)=G’(A)=0 и F’(X) И G’(X) Удовлетворяют условиям, наложенным в теореме 3 на F(X) И G(X), к отношению ![]() можно еще раз применить правило Лопиталя:
можно еще раз применить правило Лопиталя:
![]()
И так далее.
Пример.

Правило Лопиталя можно применять и для раскрытия неопределенностей вида ![]() , то есть для вычисления предела отношения двух функций, стремящихся к бесконечности при
, то есть для вычисления предела отношения двух функций, стремящихся к бесконечности при ![]()
Теорема 4. Пусть функции F(X) и G(X) непрерывны и дифференцируемы при ![]() в окрестности точки А, причем
в окрестности точки А, причем ![]() в этой окрестности. Тогда, если
в этой окрестности. Тогда, если
![]()
И существует

То существует и
![]()
Причем

Доказательство.
Выберем в рассматриваемой окрестности точки А Точки A и Х Так, чтобы A < X < A (или A < X < A). Тогда по теореме Коши существует точка С (A < C < X) такая, что
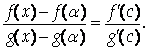
Так как
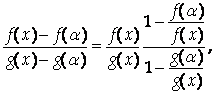
Получаем:
 .
.
Так как

Можно для любого малого E выбрать A настолько близким к А, что для любого С будет выполняться неравенство
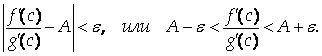
Для этого же значения ε из условия теоремы следует, что

Поэтому

Перемножим два полученных неравенства:

Или
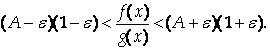
Поскольку E – произвольно малое число, отсюда следует, что
![]()
Что и требовалось доказать.
Замечание 1. Теорема 4 верна и при А=![]() . В этом случае
. В этом случае

Тогда и

Следовательно,
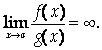
Замечание 2. Теоремы 3 и 4 можно доказать и для случая, когда ![]() .
.
Пример.

| < Предыдущая | Следующая > |
|---|