2.4.1. Теоремы Лагранжа и Коши. Правило Лопиталя

Теорема 1 (теорема Лагранжа). Если функция Y=F(X) непрерывна на отрезке [Ab] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [Ab] найдется хотя бы одна точка C, A < C < B, что

F(B) - F(A) = F′(C) (B – A).

Доказательство.

Обозначим

И рассмотрим вспомогательную функцию F(X) = F(X) - F(A) - (X - A)Q. Эта функция удовлетворяет всем условиям теоремы Ролля: она непрерывна на [Ab], дифференцируема на (Ab) и F(A)=F(B)=0. Следовательно, на интервале (Ab) есть точка С, в которой F’(C)=0. Но F’(X)=F’(X) – Q, То есть F’(C) = F’(C) – Q. Подставив в это равенство значение Q, получим

Откуда непосредственно следует утверждение теоремы.

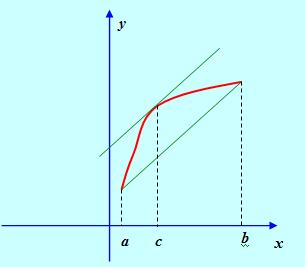
Замечание. Геометрический смысл теоремы Лагранжа: на графике функции Y = F(X) найдется точка, касательная в которой параллельна отрезку, соединяющему точки графика с абсциссами А и B.

Теорема 2 (теорема Коши). Если F(X) И G(X) – функции, непрерывные на [Ab] и дифференцируемые на (Ab), и G′(X)≠0 на (Ab), то на (Ab) найдется такая точка X=C, A<C<B, Что

Доказательство.

Обозначим

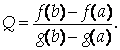
При этом G(B)-G(A) не равно нулю, иначе по теореме Ролля нашлась бы точка внутри отрезка [Ab], в которой G’(X)=0, что противоречит условию теоремы. Рассмотрим вспомогательную функцию

Для которой выполнены все условия теоремы Ролля (в частности, F(A)=F(B)=0). Следовательно, внутри отрезка [Ab] существует точка Х=с, в которой F’(C)=0. Но

Подставляя в это равенство значение Q, получаем доказательство утверждения теоремы.

< Предыдущая		Следующая >