2.3.6. Примеры решения задач по теме «Производные высших порядков»

Задача 1.

Найти вторую производную от функции

Указание

Найдите вначале первую производную данной функции, а затем воспользуйтесь тем, что

Решение

Ответ: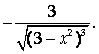

Задача 2.

Найти вторую производную от функции

При Х = 1.

Указание

Найдите вторую производную по формуле

А затем вычислите ее значение при Х = 1.

Решение

Ответ:

Задача 3.

Найти производную 4-го порядка от функции

Указание

Воспользуйтесь тем, что

Решение

Ответ:

Задача 4.

Найдите общее выражение для производной порядка П от функции

Указание

Воспользуйтесь тем, что

Решение

Вычислим подряд производные 1-го, 2-го, … порядка от данной функции и попробуем определить вид зависимости выражения для П-й производной от ее порядка.

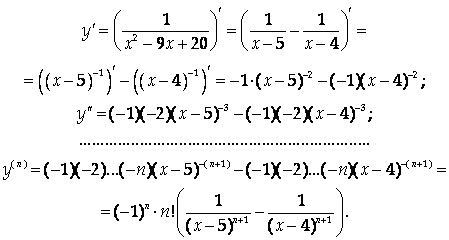
Ответ: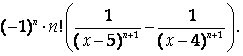

Задача 5.

Найдите общее выражение для производной порядка П от функции

Указание

Для упрощения воспользуйтесь формулами приведения:

Решение

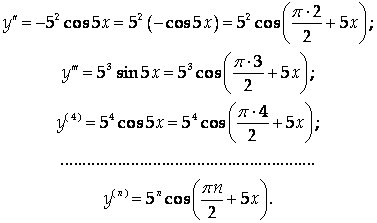
Ответ:

Задача 6.

Найти вторую производную для функции, заданной параметрически:

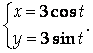
Указание

Воспользуйтесь формулой

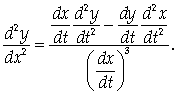
Решение

Ответ:

Задача 7.

Найти D3Y для функции У = Х5.

Указание

Воспользуйтесь формулой

Решение

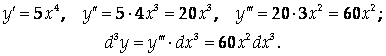
Ответ:

Задача 8.

Вычислите производную:

Указание

Воспользуйтесь формулой Лейбница:

Решение

Пусть

Тогда

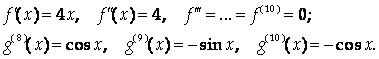
Применяя формулу Лейбница, получим:

Ответ:

Задача 9.

Рассматриваются функции

Для какой из них выполнены все условия теоремы Ролля?

Указание

По условию теоремы Ролля функция Y = F(X)

4) непрерывна на отрезке [Ab];

5) дифференцируема во всех внутренних точках этого отрезка;

6) принимает равные значения на концах этого отрезка, то есть F(A) = F(B).

Решение

Проверим выполнение условий теоремы Ролля для каждой из функций:

Не выполнено 3-е условие теоремы Ролля;

Эта функция не дифференцируема при Х = 1, то есть не выполнено 2-е условие теоремы Ролля;

3) Х = 0 – точка разрыва данной функции, то есть не выполнено 1-е условие теоремы Ролля;

Функция Y = ln cos X определена и непрерывна на заданном отрезке;

Существует на всем отрезке;

Таким образом, все условия теоремы Ролля выполнены.

Функция не является непрерывной в точке Х = 1, не выполнено 1-е условие теоремы Ролля.

Ответ: 4.

< Предыдущая		Следующая >