2.3.5. Точки экстремума функции
|
Точка Х0 называется Точкой максимума (минимума) функции Y =F(X), Если
Для всех Х из некоторой D-окрестности точки Х0 |
Точки максимума и минимума функции называются ее Точками экстремума.
Примеры.
1. Y=X² имеет минимум при Х=0.
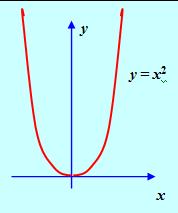
Рис. 1
2. Y=-|X-3| имеет максимум при Х=3.

Рис. 2
3. У=SinX Имеет минимумы при
![]()
И максимумы при
![]()
Теорема 1 (теорема Ферма). Если функция Y = F(X) Определена в некоторой окрестности точки Х0, принимает в этой точке наибольшее (наименьшее) в рассматриваемой окрестности значение и имеет в точке Х0 производную, то F’(X0)=0.
Доказательство.
Пусть F(X0) – наибольшее значение функции, то есть для любой точки выбранной окрестности выполняется неравенство F(X) < F(X0). Тогда, если X < X0 ,
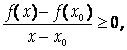
А если X > X0 ,

Переходя к пределу в полученных неравенствах, находим, что из первого из них следует, что F’(X0) > 0, А из второго – что F’(X0) < 0. Следовательно,
F′(X0) = 0.
Замечание. В теореме Ферма важно, что Х0 – внутренняя точка для данного промежутка. Например, функция Y = X, рассматриваемая на отрезке [0;1], принимает наибольшее и наименьшее значения соответственно при Х = 1 и Х = 0, но ее производная в этих точках в ноль не обращается.
Теорема 2 (теорема Ролля). Если функция Y = F(X)
1) непрерывна на отрезке [Ab];
2) дифференцируема во всех внутренних точках этого отрезка;
3) принимает равные значения на концах этого отрезка, то есть F(A) = F(B),
То внутри интервала (Ab) существует по крайней мере одна точка Х = с, A < C < B, Такая, что F’(C) = 0.

Рис. 3
Доказательство.
Пусть M И M – наибольшее и наименьшее значения F(X) на [Ab]. Тогда, если M = M, то F(X) = M = M – постоянная функция, и F’(X)=0 для любой точки отрезка [Ab]. Если же M<M, то по свойству функции, непрерывной на отрезке, хотя бы одно из значений M Или M достигается во внутренней точке С отрезка [Ab] (так как на концах отрезка функция принимает равные значения). Тогда по теореме Ферма F’(C) = 0.
Замечание 1. В теореме Ролля существенно выполнение всех трех условий. Приведем примеры функций, для каждой из которых не выполняется только одно из условий теоремы, и в результате не существует такой точки, в которой производная функции равна нулю.
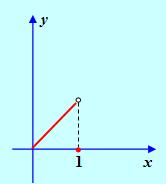
Рис. 4
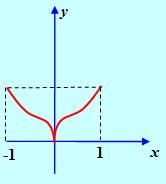
Рис. 5

Рис. 6
Действительно, у функции, график которой изображен на рис. 4, F(0)=F(1)=0, Но Х=1 – точка разрыва, то есть не выполнено первое условие теоремы Ролля. Функция, график которой представлен на рис.5, не дифференцируема при Х = 0, а для третьей функции F(-1) не равно F(1).
Замечание 2. Геометрический смысл теоремы Ролля: на графике рассматриваемой функции найдется по крайней мере одна точка, касательная в которой параллельна оси абсцисс.

Рис. 7
| < Предыдущая | Следующая > |
|---|