4.2. Условный экстремум

Экстремум функции, найденный при условии, что изменения ее аргументов ограничены некоторыми дополнительными уравнениями, называется Условным экстремумом.

Уравнения, налагающие ограничения (связи) на аргументы данной функции, называются Уравнениями связей. Геометрически это будут уравнения некоторых кривых или поверхностей.

Найти экстремум функции при условии , означает отыскание экстремальных значений аппликат вдоль кривой .

Найти экстремум функции при условии , означает отыскание такой точки на поверхности , в которой имеет наибольшее или наименьшее значение по сравнению с ее значениями в остальных точках поверхности , лежащих в достаточно малой -окрестности точки .

Значение функции в точке называется Условным максимумом, если эта точка удовлетворяет дополнительным уравнениям и если существует такая ее -окрестность, для всех точек которой, удовлетворяющих тем же уравнениям , будет выполняться неравенство · Сама точка называется в этом случае Точкой условного максимума.

Аналогично определяется Условный минимум и Точка условного минимума, в которой .

Если уравнения связи разрешены относительно некоторых переменных, то, подставляя эти переменные в уравнение функции, можно уменьшить число связей либо вовсе избавиться от связей и решать задачу о безусловном экстремуме.

Для нахождения экстремума функции двух переменных при условии в уравнение функции, получим задачу на экстремум для функции одной переменной .

Пример 20. Найти экстремум функции при условии .

Решение. Из уравнения связи находим .

Тогда

.

, , , .

Так как , то - точка минимума.

Тогда ,

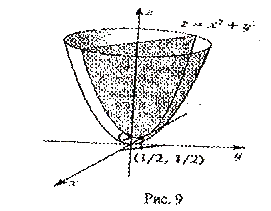
Т. е. при аргументах, удовлетворяющих уравнению связи , (рис. 9).

Если уравнение связи не разрешимо ни относительно ни одной из переменных, то для нахождения условного экстремума используют метод множителей Лагранжа.

< Предыдущая		Следующая >