4.1. Экстремум функции двух переменных. Необходимые и достаточные условия существования экстремума
Пусть функция двух переменных ![]() задана в некоторой области
задана в некоторой области ![]() .
.
Точка ![]() называется Точкой максимума функции
называется Точкой максимума функции ![]() , если существует такая окрестность этой точки, что для всех точек
, если существует такая окрестность этой точки, что для всех точек ![]() этой окрестности, отличных от
этой окрестности, отличных от ![]() , выполняется неравенство
, выполняется неравенство ![]() (рис. 7).
(рис. 7).
Точка ![]() называется Точкой минимума функции
называется Точкой минимума функции ![]() , если существует такая окрестность этой точки, что для всех точек
, если существует такая окрестность этой точки, что для всех точек ![]() этой окрестности, отличных от
этой окрестности, отличных от ![]() , выполняется неравенство
, выполняется неравенство ![]() (рис. 8).
(рис. 8).
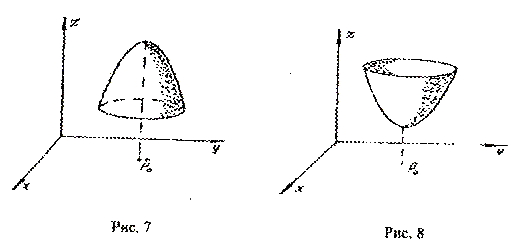
Как и в случае функции одной переменной, точка максимума (или минимума) не следует смешивать с точкой, в которой функция принимает наибольшее (или наименьшее) значение в области ![]() .
.
Значение функции ![]() в точке максимума (точке минимума) называют Максимумом (Минимумом) функции или экстремумом.
в точке максимума (точке минимума) называют Максимумом (Минимумом) функции или экстремумом.
Теорема (необходимый признак существования экстремума). Если ![]() есть точка экстремума функции
есть точка экстремума функции ![]() , то
, то
![]() ,
, ![]()
В предположении, что указанные частные производные существуют в точке ![]() .
.
Таким образом, Обращение в нуль в точке ![]() Частных производных первого порядка функции
Частных производных первого порядка функции ![]() (если они существуют) является Необходимым условием существования в точке
(если они существуют) является Необходимым условием существования в точке ![]() экстремума этой функции.
экстремума этой функции.
Функция может иметь экстремум также в тех точках, где хотя бы одна из частных производных не существует. Например, функция ![]() , очевидно, имеет минимум в точке
, очевидно, имеет минимум в точке ![]() , но в этой точке частные производные
, но в этой точке частные производные ![]() и
и ![]() не существуют.
не существуют.
Точки, в которых частные производные первого порядка ![]() ,
, ![]() обращаются в ноль или не существуют, называются Критическими точками этой функции.
обращаются в ноль или не существуют, называются Критическими точками этой функции.
Из изложенного выше следует, что точка экстремума функции следует искать среди ее критических точек. Однако не всякая критическая точка будет точкой экстремума функции.
Теорема (достаточный признак существования экстремума). Пусть ![]() - критическая точка функции
- критическая точка функции ![]() .
.
Обозначим ![]() ,
, ![]() ,
, ![]() и составим
и составим ![]() .
.
Тогда, если ![]() , то
, то ![]() - точка экстремума, причем
- точка экстремума, причем
![]() - точка максимума в случае
- точка максимума в случае ![]() ,
,
![]() - точка минимума в случае
- точка минимума в случае ![]() ,
,
Если ![]() , то в точке
, то в точке ![]() - экстремума нет,
- экстремума нет,
Если ![]() , то требуется дополнительные исследования (сомнительный случай).
, то требуется дополнительные исследования (сомнительный случай).
Пример 19. Найти экстремумы функции ![]() .
.
Решение. Найдем частные производные первого порядка:
![]() ,
, ![]() .
.
Приравнивая эти производные к нулю, после элементарных преобразований получим систему уравнений:
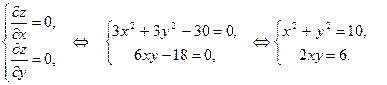
Складывая и вычитая почленно уравнения системы, получим:
 или
или  или
или ![]()
Решая эту систему уравнений (равносильную данной), находим четыре критические точки: ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
Теперь найдем частные производные второго порядка:
![]() ,
, ![]() ,
, ![]() ,
,
Составим выражение ![]() .
.
Так как
1. ![]() - точка минимума;
- точка минимума;
2. ![]() В точке
В точке ![]() Экстремума нет;
Экстремума нет;
3. ![]() В точке
В точке ![]() Экстремума нет;
Экстремума нет;
4. ![]() - точка максимума.
- точка максимума.
Итак, данная функция имеет два экстремума:
В точке ![]() - минимум
- минимум ![]() ,
,
В точке ![]() - максимум
- максимум ![]() .
.
| < Предыдущая | Следующая > |
|---|