4.3. Наибольшее и наименьшее значения функции в замкнутой области

Пусть функция непрерывна в ограниченной замкнутой области и дифференцируема внутри этой области.

Тогда она имеет в этой области наименьшее и наибольшее значения, которые достигаются либо внутри области, либо на ее границе.

Если наибольшее или наименьшее значения функции принимает во внутренних точках области , то эти точки, очевидно, являются точками экстремума функции .

Таким образом, точки, в которых функция имеет наибольшее или наименьшее значения, являются либо точками экстремума, либо граничными точками области .

Алгоритм нахождения наибольшего и наименьшего значений функции двух переменных.

1. Находим критические точки функции в области из условий: , . Вычисляем значения функции в этих точках.

2. Находим наибольшее и наименьшее значения функции на границе области .

3. Сравнивая все полученные в п. п. 1, 2 значения функции , выбираем наибольшее и наименьшее.

В некоторых случаях при нахождении наибольших и наименьших значений функции двух переменных в ограниченной замкнутой области границу этой области удобно разбить на части, каждая из которых задается своим уравнением.

Пример 21. найти наибольшее и наименьшее значения функции

.

В замкнутом треугольнике , , .

Решение.

1. Найти критические точки функции внутри области :

, , т. е.

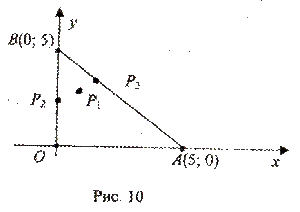
Получили критическую точку (см. рис. 10).

Вычислим значения функции .

2. Исследуем функцию на границе области:

I. рассмотрим участок : , , ,

, .

Тогда наибольшее и наименьшее значения функции может принимать на концах отрезка .

Вычислим .

II. рассмотрим участок : , , ,

, .

Получили точку (рис. 10).

Вычислим значения функции в найденной точке и на концах отрезка :

,.

III. Рассмотрим участок : ,

,

, .

Получили точку (рис. 10).

Вычислим .

Обобщая полученные результаты имеем:

, , ,

, ,

Следовательно ; .

< Предыдущая