3.2. Градиент функции
При изучении скалярных полей наряду с функций ![]() рассматривается некоторый вектор, тесно связанный с этой функцией, - градиент скалярного поля.
рассматривается некоторый вектор, тесно связанный с этой функцией, - градиент скалярного поля.
Градиентом в точке ![]() скалярного поля, заданного дифференцируемой функцией
скалярного поля, заданного дифференцируемой функцией ![]() , называется вектор, равный
, называется вектор, равный
![]() .
.
Таким образом, каждой точке ![]() скалярного поля, заданного дифференцируемой функцией
скалярного поля, заданного дифференцируемой функцией ![]() , соответствует не только значение этой функции, но и вполне определенный вектор
, соответствует не только значение этой функции, но и вполне определенный вектор ![]() .
.
Между градиентом функции в данной точке и производной по направлению в той же точке имеется связь, которая устанавливается следующей теоремой.
Теорема. Проекция вектора ![]() На единичный вектор
На единичный вектор ![]() равна производной функции
равна производной функции ![]() по направлению
по направлению ![]() :
:
![]() .
.
Доказательство. Пусть ![]() . Из векторной алгебры известно, что проекция какого-либо вектора на другой вектор равна скалярному произведению этих векторов.
. Из векторной алгебры известно, что проекция какого-либо вектора на другой вектор равна скалярному произведению этих векторов.
Так как 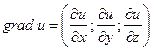 ,
, ![]() , то
, то
![]() .
.
Учитывая, что производная по направлению ![]() выражает скорость изменения скалярного поля
выражает скорость изменения скалярного поля ![]() в этом направлении, можно сказать, что проекция
в этом направлении, можно сказать, что проекция ![]() на вектор
на вектор ![]() равна скорости изменения поля
равна скорости изменения поля ![]() в направлении вектора
в направлении вектора ![]() .
.
Обозначим через ![]() угол между единичным вектором
угол между единичным вектором ![]() и
и ![]() . Тогда
. Тогда ![]() .
.
Поэтому ![]() .
.
Если направления векторов ![]() и
и ![]() совпадают (
совпадают (![]() ), то производная по направлению
), то производная по направлению ![]() имеет, очевидно, наибольшее значение, равное
имеет, очевидно, наибольшее значение, равное ![]() .
.
Таким образом, ![]() есть вектор, указывающий Направление наибольшего возрастания поля в данной точке и имеющий Модуль равный скорости этого возрастания.
есть вектор, указывающий Направление наибольшего возрастания поля в данной точке и имеющий Модуль равный скорости этого возрастания.
Рассмотрим кривую ![]() , лежащую на поверхности уровня
, лежащую на поверхности уровня ![]() и проходящую через точку
и проходящую через точку ![]() . Градиент функции
. Градиент функции ![]() в точке
в точке ![]() обладает следующими свойствами:
обладает следующими свойствами: ![]() перпендикулярен к вектору
перпендикулярен к вектору ![]() , направленному по касательной к кривой
, направленному по касательной к кривой ![]() в точке
в точке ![]() .
.
В случае плоского скалярного поля, заданного дифференцируемой функцией двух переменных ![]() , градиент определяется формулой
, градиент определяется формулой
![]() .
.
Его связь с производной по направлению ![]() выражается равенством
выражается равенством
![]() ,
,
Где ![]() - угол между единичным вектором
- угол между единичным вектором ![]() и
и ![]() . Вектор
. Вектор ![]() перпендикулярен к касательной, проведенной к линии уровня в точке
перпендикулярен к касательной, проведенной к линии уровня в точке ![]() .
.
Пример 16. Найти наибольшую скорость возрастания функции
![]() в точке
в точке ![]() .
.
Решение. Наибольшая скорость возрастания функции равна модулю градиента этой функции. Найдем градиент функции ![]() :
:
![]() ,
, ![]()
![]() .
.
В точке ![]() имеем
имеем ![]() .
.
Тогда наибольшая скорость возрастания функции равна
![]() .
.
Пример 17. Найти скорость изменения скалярного поля, определяемого функцией ![]() в точке
в точке ![]() в направлении касательной, проведенной к параболе
в направлении касательной, проведенной к параболе ![]() в этой точке в сторону возрастания координаты
в этой точке в сторону возрастания координаты ![]() , и наибольшую скорость изменения поля в этой точке.
, и наибольшую скорость изменения поля в этой точке.
Решение. Скорость изменения скалярного поля в заданном направлении есть производная скалярного поля ![]() по направлению вектора
по направлению вектора ![]() , задающего направление.
, задающего направление.
![]() ,
,
Где 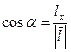 ;
;  - направляющие косинусы вектора
- направляющие косинусы вектора ![]() ,
, ![]() . Вектор
. Вектор ![]() возьмем на касательной к параболе
возьмем на касательной к параболе ![]() в
в ![]() , для чего составим уравнение касательной
, для чего составим уравнение касательной
![]() ,
,
![]() ,
, ![]()
![]() - уравнение касательной.
- уравнение касательной.
На найденной касательной возьмем точку ![]() с любой координатой
с любой координатой ![]() (
(![]() ), например
), например ![]() . Тогда
. Тогда
![]() .
.
Найдем значения производной по направлению в точке ![]() :
:
![]() ,
,
![]() .
.
Тогда ![]() .
.
Наибольшая скорость изменения поля в точке ![]() есть
есть ![]() .
.
Так как ![]() , то
, то
![]() .
.
Величина наибольшей скорости
![]() .
.
| < Предыдущая | Следующая > |
|---|